filmov
tv
Minimum Spanning Trees with Prim's and Kruskal's Algorithms

Показать описание
A complete graph with three or more nodes is full of cycles allowing multiple paths or walks between nodes or vertices. When a weight is added to each edge of a walk, we can determine the optimal walk. This has applications ranging from networking to travel planning.
After defining spanning trees, weighted graphs, and minimum spanning trees, we present the Prim and Kruskal algorithms, two tools we can use to determine the minimum spanning tree from a connected graph.
Timestamps
00:00 | Intro
00:16 | Tree review
01:27 | Spanning tree description
02:40 | Spanning trees from complete graphs
04:56 | Ethernet "Time to Live" element
06:04 | Weighted graph description
09:15 | What could the weights represent?
10:13 | Minimum spanning tree description
11:53 | Presenting a complete graph example - airline connections
13:28 | Prim's algorithm description
15:24 | Prim's algorithm example
18:06 | Kruskal's algorithm description
19:44 | Kruskal's algorithm example
Hashtags
#tree #prim #kruskal
After defining spanning trees, weighted graphs, and minimum spanning trees, we present the Prim and Kruskal algorithms, two tools we can use to determine the minimum spanning tree from a connected graph.
Timestamps
00:00 | Intro
00:16 | Tree review
01:27 | Spanning tree description
02:40 | Spanning trees from complete graphs
04:56 | Ethernet "Time to Live" element
06:04 | Weighted graph description
09:15 | What could the weights represent?
10:13 | Minimum spanning tree description
11:53 | Presenting a complete graph example - airline connections
13:28 | Prim's algorithm description
15:24 | Prim's algorithm example
18:06 | Kruskal's algorithm description
19:44 | Kruskal's algorithm example
Hashtags
#tree #prim #kruskal
3.5 Prims and Kruskals Algorithms - Greedy Method
Prim's Algorithm
L-4.9: Prim's Algorithm for Minimum Cost Spanning Tree | Prims vs Kruskal
How does Prim's Algorithm work? #shorts
Prim's Minimum Spanning Tree Algorithm | Graph Theory
#2 Prims Algorithm Minimum | How to find Spanning Tree Greedy Search Algorithm by Dr. Mahesh Huddar
How Do You Calculate a Minimum Spanning Tree?
Prim's Algorithm for Minimum Spanning Trees (MST) | Graph Theory
NPTEL Design and analysis of algorithms Week 1 Assignment 1 Answers Solution Quiz | 2025 - Jan
Networks: Prim's Algorithm for finding Minimum spanning trees
Prim's Algorithm for Creating a Minimum Spanning Tree (MST) - Min Cost to Connect Points (LC 15...
Minimum Cost Spanning Trees Prims Algorithm
31251 Lecture 12.1: Minimum spanning trees and Prim's algorithm
Prim's Algorithm: Minimal Spanning Tree
Prim's Algorithm - Minimum Spanning Tree - Min Cost to Connect all Points - Leetcode 1584 - Pyt...
Prim's Algorithm | Minimum Spanning tree | MST | DAA | Lec-26 | Bhanu Priya
Prim's Algorithm for Minimum Spanning Tree | Graph Theory #13
Kruskal's Algorithm: Minimum Spanning Tree (MST)
OCR MEI MwA E: Minimum Spanning Trees: 04 Prim’s Algorithm Example 1
Prim's Algorithm to Find Minimum Spanning Tree Example
Proof of Prim's MST algorithm using cut property
Min Cost to Connect All Points - Minimum Spanning Tree (MST) - Leetcode 1584
G-45. Prim's Algorithm - Minimum Spanning Tree - C++ and Java
Prims Algorithm Minimum Spanning Tree
Комментарии
 0:20:12
0:20:12
 0:07:18
0:07:18
 0:09:55
0:09:55
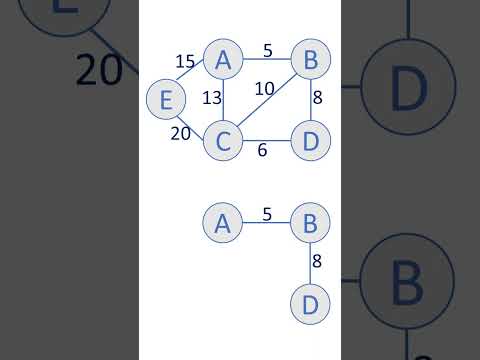 0:00:49
0:00:49
 0:14:53
0:14:53
 0:05:42
0:05:42
 0:11:12
0:11:12
 0:11:32
0:11:32
 0:01:32
0:01:32
 0:07:40
0:07:40
 0:00:47
0:00:47
 0:22:35
0:22:35
 0:28:47
0:28:47
 0:06:46
0:06:46
 0:22:08
0:22:08
 0:13:02
0:13:02
 0:18:29
0:18:29
 0:06:01
0:06:01
 0:05:34
0:05:34
 0:05:15
0:05:15
 0:08:21
0:08:21
 0:00:38
0:00:38
 0:19:10
0:19:10
 0:04:57
0:04:57