filmov
tv
Integral of Sqrt(9 - x^2) by Trigonometric Substitution | Integration | Calculus | Glass of Numbers
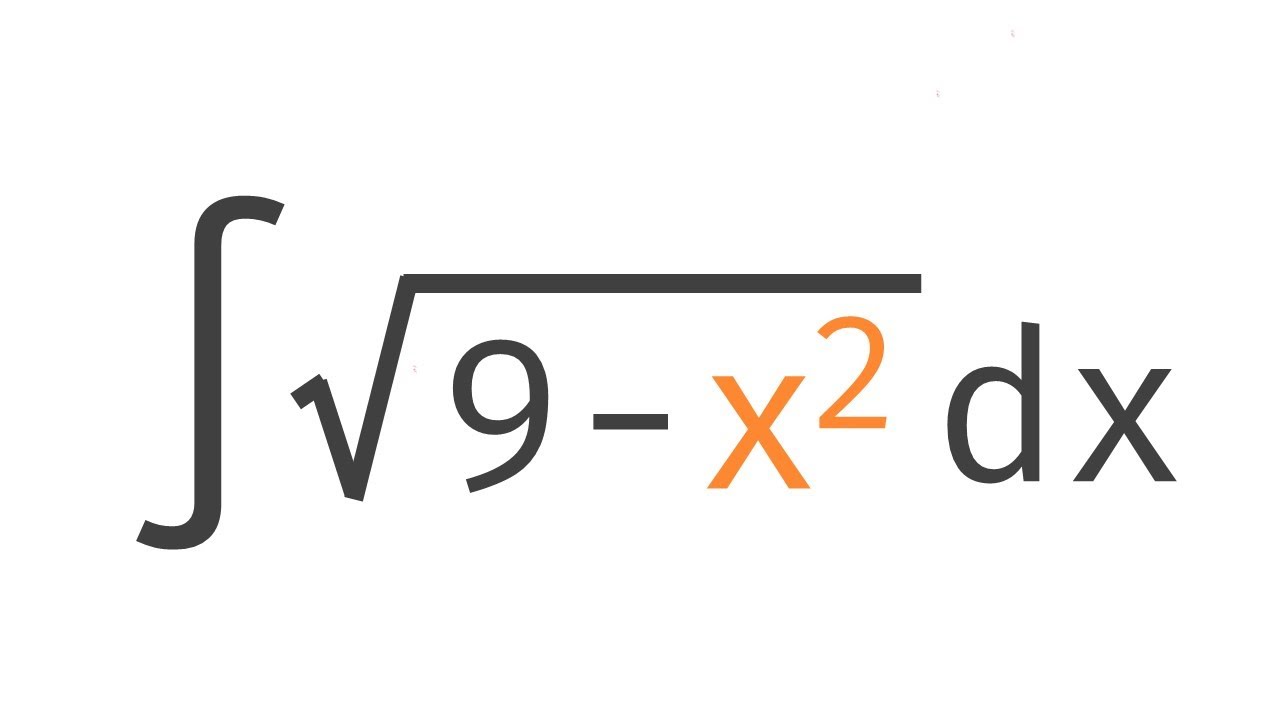
Показать описание
In this video, we integrate a function involving a square root by using trigonometric substitution. (We often call this "trig sub" or "trig sub integral".)
Depending on the form of the expression inside the square root, we will make the following substitution using a trigonometric function:
For A^2 - X^2, we use X = A sinθ.
For A^2 + X^2, we use X = A tanθ.
For X^2 - A^2, we use X = A secθ.
After performing the trig sub, we need to integrate cosine squared of theta: cos^2(θ). See how to do that integral here:
📺 Subscribe to my channel for Math Learning!
Please help me by subscribing to my YouTube channel. I want to use my free time to make a lot of math videos to help others and to make education available to the world. Your Likes and Subscribing will help this channel be reached by more people. Thank you!
Follow me:
Ayúdame suscribiéndome a mi canal de YouTube. Quiero usar mi tiempo libre para hacer muchos videos de matemáticas para ayudar a otros y hacer que la educación esté disponible para el mundo. Tus Me gusta y Suscripciones ayudarán a que más personas lleguen a este canal. ¡Gracias!
請訂閱我的YouTube Channel, 我會製作更多與數學相關的視頻,讓世界各地的朋友用簡單的方法學習數學(數學考試一定A)!請用您的訂閱和點贊支持我,並在留言區與我討論!謝謝!
#Calculus #Integration #Integral
Depending on the form of the expression inside the square root, we will make the following substitution using a trigonometric function:
For A^2 - X^2, we use X = A sinθ.
For A^2 + X^2, we use X = A tanθ.
For X^2 - A^2, we use X = A secθ.
After performing the trig sub, we need to integrate cosine squared of theta: cos^2(θ). See how to do that integral here:
📺 Subscribe to my channel for Math Learning!
Please help me by subscribing to my YouTube channel. I want to use my free time to make a lot of math videos to help others and to make education available to the world. Your Likes and Subscribing will help this channel be reached by more people. Thank you!
Follow me:
Ayúdame suscribiéndome a mi canal de YouTube. Quiero usar mi tiempo libre para hacer muchos videos de matemáticas para ayudar a otros y hacer que la educación esté disponible para el mundo. Tus Me gusta y Suscripciones ayudarán a que más personas lleguen a este canal. ¡Gracias!
請訂閱我的YouTube Channel, 我會製作更多與數學相關的視頻,讓世界各地的朋友用簡單的方法學習數學(數學考試一定A)!請用您的訂閱和點贊支持我,並在留言區與我討論!謝謝!
#Calculus #Integration #Integral
Комментарии
 0:05:06
0:05:06
 0:16:11
0:16:11
 0:10:32
0:10:32
 0:04:43
0:04:43
 0:07:04
0:07:04
 0:05:40
0:05:40
 0:22:27
0:22:27
 0:09:51
0:09:51
 0:04:27
0:04:27
 0:14:23
0:14:23
 0:09:20
0:09:20
 0:26:02
0:26:02
 0:06:55
0:06:55
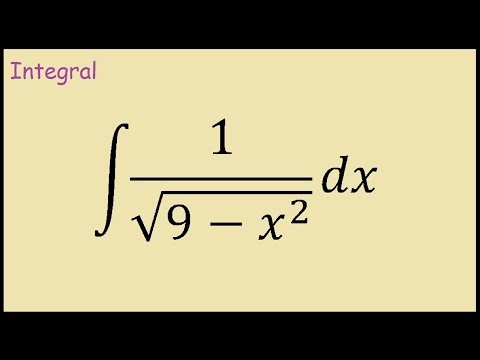 0:03:19
0:03:19
 0:10:13
0:10:13
 0:00:55
0:00:55
 0:05:13
0:05:13
 0:06:51
0:06:51
 0:08:39
0:08:39
 0:09:37
0:09:37
 0:08:31
0:08:31
 0:09:20
0:09:20
 0:12:15
0:12:15
 0:11:35
0:11:35