Numbers too big to imagine

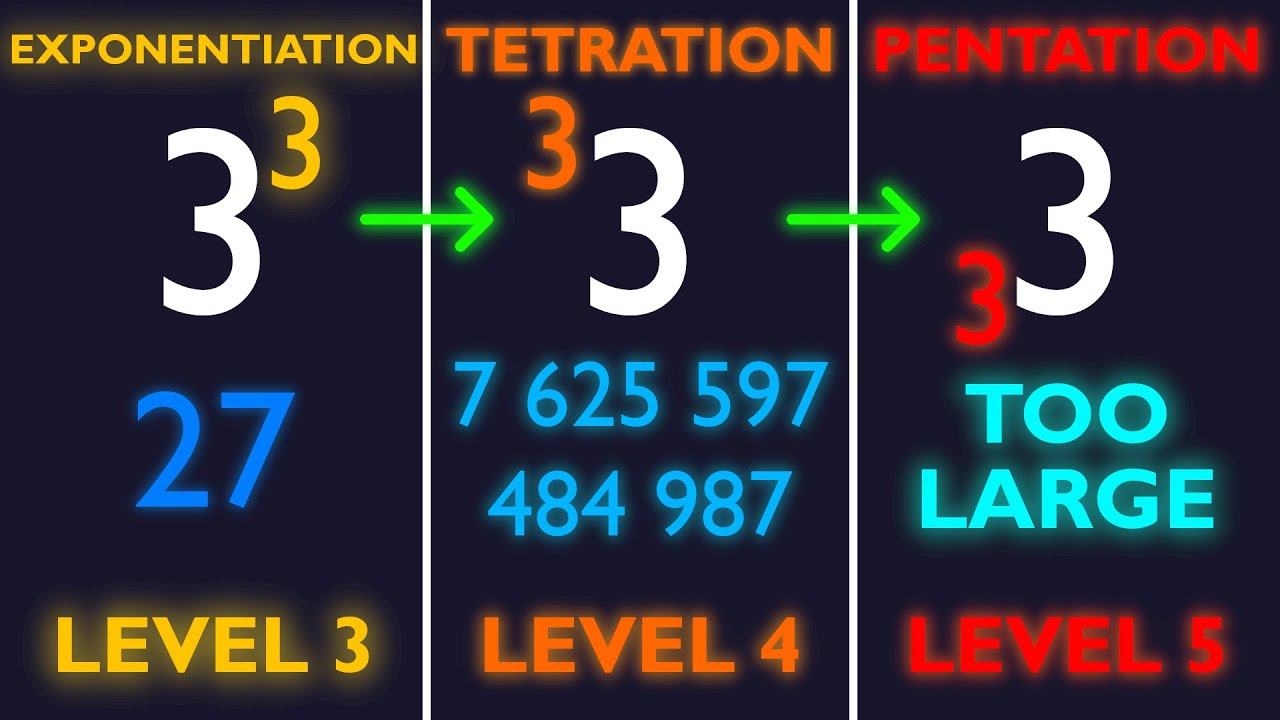
In mathematics, tetration is an operation based on iterated, or repeated, exponentiation. By using operations such as tetration, pentation or hexation we can create enormous numbers. Graham’s number is one of the most famous big numbers, but there are many even bigger numbers.

Chapters:
00:00 First Hyperoperations
00:35 Tetration
01:26 Infinite Towers
02:12 Higher-level operations
03:23 Graham's Number
04:45 TREE(3)
07:00 Giant Numbers

Music:
@AlekseyChistilin

[digitalgenius]

From 7:26 all the greater-than signs (">") should be pointing in the other direction ("<"). Sorry for the mistake.

[ChessGrandPasta]

it still amazes me to think that if you were to pick a random positive integer the chance that it's bigger than Graham's number tends to 100%.

[shawnheim]

Tree 1: 1
Tree 2: 3
Tree 3: Unimaginably huge number beyond the realm of human comprehension

[soup]

I find it funny how TREE(1) is 1, TREE(2) is 3, and TREE(3) is some ungodly huge number.

[_Norv]

Finally, a good way to measure the ratio of chips to air in a lay’s packet of chips.

[ashagupta]

And still, all of them are closer to zero than infinity

[zbwcrzf]

Even though TREE(3) completely dwarfs g63, I love Graham's Number because you can somewhat appreciate just how insanely massive it is when you express it in terms of how many 3s and exponentiation towers exist even just in g(0). In comparison, the tree function is like... "Yeah here's some confusing rules, we go from 1, to 3, to practically-but-not-quite forever"

[nidadursunoglu]

The fact that its easier to imagine infinity than a really big number is insane. Its easy to know infinity goes forever but its almost impossible how big would a pile of 7 tetrated by 7 number of apples

[moonbeamskies]

I can personally attest to the fact that tree(3) is a large number because I stayed up all night with pens and paper testing it by drawing trees and I never came to the end. I had well over 400 trees drawn in that time and didn't seem to be near the end of possible trees. I fell asleep and dreamed of trees combinations.😮

[livingthemcdream]

Just so you know, you just explained exponentiation better than literally every teacher I have had up until now in less than 30 seconds

[marasmusine]

I do like how we can't write down Graham's number even if we inscribed a digit on every particle in the visible universe, but we do know what digits it ends in (last digit is 7).

[RoyaltyInTraining.]

I never thought a number could scare me, but G1 is already so stupidly and mindbogglingly big that it does the trick.

[EnerJetix]

This video felt like a combination of Numberphile’s videos on the topics, but with neat animation as visuals instead. Very well done

[niviera]

I opened YouTube to listen to some music and here i am watching a man teaching me math

[KiatHuang]

The best exposition I've seen so far on large numbers with precise descriptions and excellent graphics. The narrator's voice is perfect for describing mathematics in English. At university I always preferred maths lecturers who did not have English as their mother tongue - less fluff, focus on diction.

[mike.]

I get that the TREE concept is a bit hard to describe, but I feel like some semblance of how we know it is finite yet much larger than Graham's number would have been appreciated.

[ycajal]

This is mind-boggling in so many tree levels

[caspermadlener]

The general way to construct enormous numbers like this is:
1. Pick a HUGE ordinal. You have to be able to prove that it is well-ordered, so it can't be infinite, it should be recursive.
2. Make a function based on thay ordinal.

Ordinals are complex subjects, but necessary at the "basis" of mathematics (which is not an important part).
For every concrete rule to create ordinals, there is a unique ordinal that can't be created with this rule.

Graham's function doesn't use that big of an ordinal, since its definition is very straightforwards. The ordinal should even be described by Peano axioms.
But the TREE function uses the small Veblen ordinal. That is quite a big ordinal.

[EdithKFrost]

Math teacher: Please find the next term of the sequence: 1, 3, …
People who know the game of trees: 😢

[DutchFurnace]

The Toddler's Theorem is the biggest number ever. "Your number, +1!"