filmov
tv
Geometric series: sum of Powers of 1/7 (visual proof)

Показать описание
This is a short, animated visual proof demonstrating the infinite sum of the powers of 1/7. #mathshorts #mathvideo #math #calculus #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #geometricseries #series #infinitesums #infiniteseries
To learn more about animating with manim, check out:
____________________________________________
Music is in the video:
Creative Commons Attribution-ShareAlike 3.0 Unported
To learn more about animating with manim, check out:
____________________________________________
Music is in the video:
Creative Commons Attribution-ShareAlike 3.0 Unported
Geometric series: sum of powers of 1/4 (visual proof)
Geometric series: sum of powers of 1/3 (visual proof)
Geometric series: sums of powers of 8 (visual proof)
Geometric series: sum of Powers of 1/7 (visual proof)
Geometric Series: sum of powers of 1/6 (visual proof)
Geometric series: sum of powers of 1/5 (visual proof)
Geometry behind the geometric sum of powers of 1/3!
Geometric series: sum of powers of 1/9 (visual proof)
Geometric series: sum of powers of 1/2 (visual proof)
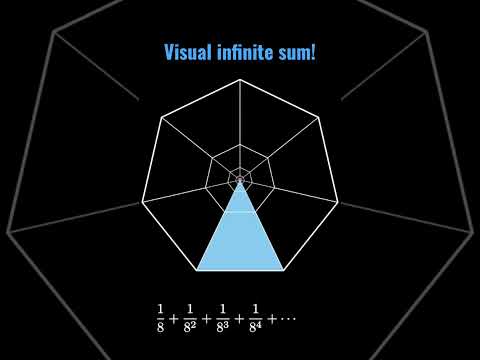
Summing powers of 1/8 visually!
Geometric Series: sum of powers of 1/8 (visual proof)
Geometric sum of powers of 7
Geometric series: sum of powers of 4/9 (visual proof)
Geometric series: sum of powers of 1/5 II (visual proof)
Geometric series: sums of powers of 3 (visual proof)
Infinite sum of powers of sixths!
Geometric Series: sum of powers of 1/9 (visual proof)
Infinite sum of powers of 4/9
Geometric series: sum of powers of 1/3 II (visual proof)
Geometry of sums of powers of 1/5
Geometric series: sums of powers of 9 are Triangular (visual proof)
Alternating Geometric Series: sum of Powers of 1/2 (visual proof)
Geometric Series: Alternating Sum of Powers of 1/4 (visual proof)
A visual infinite sum like you’ve never seen!
Комментарии
 0:01:06
0:01:06
 0:01:49
0:01:49
 0:01:48
0:01:48
 0:02:42
0:02:42
 0:01:32
0:01:32
 0:02:05
0:02:05
 0:01:00
0:01:00
 0:01:50
0:01:50
 0:01:17
0:01:17
 0:00:53
0:00:53
 0:01:13
0:01:13
 0:01:00
0:01:00
 0:01:28
0:01:28
 0:02:04
0:02:04
 0:01:30
0:01:30
 0:00:55
0:00:55
 0:01:41
0:01:41
 0:00:52
0:00:52
 0:01:18
0:01:18
 0:00:53
0:00:53
 0:01:48
0:01:48
 0:01:28
0:01:28
 0:01:26
0:01:26
 0:00:57
0:00:57