Incircle area in 3-4-5 triangle?

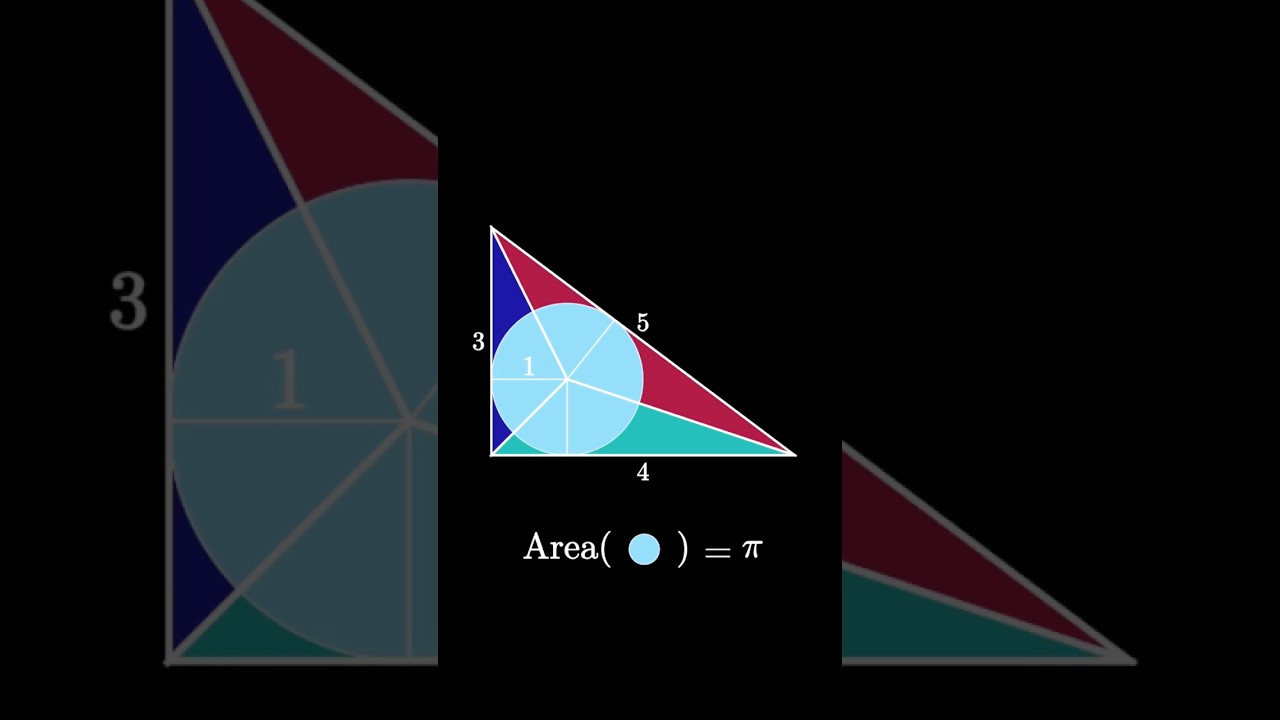
This short demonstrates an intriguing fact about the area of the incircle of the 3-4-5 right triangle. Using two different methods of computing the area of the 3-4-5 rectangle, we find that the inradius has a length of one so that the area of the incircle is Pi!

Thanks!

#manim #math #mathvideo #mathshorts #geometry #circle #triangle #animation #theorem #pww #proofwithoutwords #visualproof #proof #incircle #inradius #incircle #semiperimeter #incenter #pi #righttriangle #area

To learn more about animating with manim, check out:

[chixenlegjo]

This works for all triangles, too. If you know the area and perimeter, you can find the radius and area of the incircle.

[KimTiger]

What I find beautiful with this is the simplicity that it contain soo many things in it.
1 = radius of max sized circle within the triangle
2 = diameter of max sized circle within the triangle
3 = opposite side of the triangle
4 = adjacent side of the triangle
5 = hypotenuse of the triangle
6 = area of the triangle
7 = ???
pi = area of the circle

[Invincible]

There is also a result for right-triangles that radius of incircle is area of right-angled triangle/semi-perimeter of that right-angled triangle. Same can be observed from that too.

[vennstudios]

if we do it for 5 now

it's
r(5-(4-r))=r(1+r) or r(r+1)
r(5-(3-r))=r(2+r) or r(r+2)
then
r²

combined them into

r²+r(r+1)+r(r+2)=6 again
simplified
r²+r²+r²+3r=6
simplified again
3r²+3r=6 simplified
r²+r=2
r²+r-2=0
(r+2)(r-1)

WHICH FINALLY GIVES US
POSITIVE 1

and followed with the fool
the Negative 2

[the-boy-who-lived]

This is the most basic right triangle we know. And having the most basic unit cricle from it made me surprised.

Edit: A 3-4-5 right triangle is special because it is the simplest Pythagorean triple

[marcelluswallace]

I figured it out not via the area but simply by getting r from a system of 3 equations with 3 unknowns.

The 3 radii shown disect the triangle into 3 kites and we know that 2 of the adjecent sides of kites always have the same length. Hence you can make a set of 3 equations:
x+r=3
y+r=4
x+y=5
solving for x and y in eq 1 and 2 and inserting in eq 3 gives
3-r+4-r=5
7-2r=5
2=2r
r=1
q.e.d.

[ashb]

You can do this also by using the square of side length r you drew and the fact that tangent segments are of equal length.

So, 3-r + 4-r = 5… then r=1

If you do the next triple, 5-12-13, you get r=2

And if you do the next, 7-24-25, you get r=3

And so on.

[heardit]

In fact, as already mentioned, this works for all triangles, if you know the area A, the side lengths a, b, c, and the perimeter p= a + b + c, you get that A = 1/2 r*a +1/2 r*b + 1/2 r*c, where r is the radius of the circle, which simplified gives 2A = r(a+b+c) => r = 2A/(a+b+c) since the area of circle is πr² =>Ac=4π(A/(a+b+c))² where Ac is the area of the circle

[naved]

Another simple solution is :-

1. The square that is made has length = r

2. So the other sides of the square will also be equal to r


3. Hence we can write that
The length of tangents = 3-r and 4-r

4.by tangent theorem we know that we can write the hypotenuse as 4-r+3-r = 5 so 2r= 7-5 hence r= 1

[reportedstolen]

We should start calling this the “unit right triangle” from now on lol

[Író-qd]

The radius of the inscribed circle of a right triangle is the base + height - hypotenuse divided by 2.
3+4−5=2, 2÷2=1=r.

[mathmachine]

(r, r) is the center. The distance from there to the hypotenuse is the dot product between the normal vector and a line between the center and literally any point on the line. <3/5, 4/5>•<4-r, -r> = 12/5-3r/5-4r/5=12/5-7r/5. 12/5-7r/5=r, 12/5=12r/5, r=1. The radius is 1, the area is π.

[oguzhanalhan]

You can find it by also saying that the lines that touch the circle are the same length from the corners of the triangle so lets just say that the length of the line that reaches from the corner of 3 and 4 is x and if you write the lenghts as 4-x, 4-x, 1+x and so on you will find that 1+2x=3 and therefore x=1. İf we draw a line from the centre of the circle towards the lines of the triangle wher it touches the circle those lines are have a 90° ont he sides. So there is a square there. Therefore x=r=1

[quokka_yt]

Another way we can go about this

First, we find the surface area of the triangle:

S∆ = (3 ⋅ 4) / 2 =
= 6

Now we find the semiperimeter:

p = (3 + 4 + 5) / 2 =
= 6

Now we use this formula:

S = pr
6 = 6r ⟹
⟹ r = 1

Now we use the formula for the area of a circle:

So = πr² =
= π ⋅ 1² =
= π

[dot_lol]

I wish I watched this when I was in geometry

[mareau]

I worked it out by realizing that you had to be able to fit two of those circles inside a rectangle of 3x4, since one circle fits inside half of such a rectangle. Which means the diameter of the circle was half the base, or 2. Radius is half of a diameter, giving a radius of 1, giving an area of pi.

[visheshsomani]

You can prove that radius of an incircle of a right triangle is the([ sum of bases] - hypotenuse) /2

[bishiyarudesu]

Another way to find in radius would be to equate length of tangents:
4-r=5-(3-r)
4-r=2+r
r=1.

[Alekzander]

Your solution seems very elegant to me, it is a very nice way to solve a problem like this, personally I was guided by Viviani's theorem to find the radius, but for someone who does not know it it is a very nice and easy way. to address the problem

[DivineRedwood]

Why? Use geometry instead.
p = 3 - r, q = 4 - r, 5 = p + q, thus r = 1 & A = Pi.