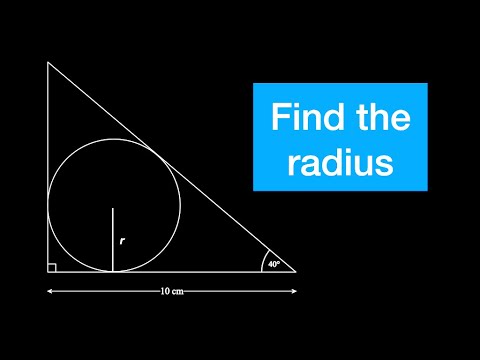
Geometry Marvels: Calculating the Incircle Area Within a Triangle

Показать описание

Prepare to embark on an exciting journey through the world of geometry with our latest video! 📐 In this tutorial, we’ll dive into the intriguing task of calculating the area of the incircle within a triangle. Join us as we demystify the mathematical techniques behind solving this captivating problem.

Our exploration will encompass:
✅ An introduction to the fundamental principles of geometry and its practical applications.
✅ A step-by-step guide to calculating the area of the incircle within a triangle.
✅ Real-world examples to illustrate the practicality of these mathematical techniques.
✅ Expert guidance to equip you with the skills to accurately compute the incircle area.

Whether you’re a student striving to excel in geometry or a math enthusiast eager to tackle fascinating geometric challenges, this video is designed to provide valuable insights and deepen your understanding of geometric relationships.

Like, share, and subscribe to our channel for more math tutorials that simplify complex concepts and offer elegant solutions to challenging problems. Get ready to master the art of calculating the area of the incircle within a triangle and elevate your mathematical expertise! 📚🌟

#Geometry #IncircleArea #MathPuzzles #Mathematics #LearnMath #StudyTips #Education #MathematicsTutorials #SubscribeNow

Рекомендации по теме

Комментарии

Nice! 5√2/2 = r(√2 + 1) → r = (5/2)(2 - √2) → r^2 = (25/2)(3 - √2) → area circle = (25π/2)(3 - √2)

murdock

I found one comparison based area based solution, the points B and C joined and the area of the triangle inside produced may be half of the right angled triangle...thus a rough estimate of r.

suindude

YOu made this way harder than it needed to be. Radius equals the (product of the legs of the triangle) divided by the (sum of the three sides of the triangle). so, r= (5x5)/5+5+5xSquare root of 2)

matts

Two more ways to calculate the radius (then the green area)
2p = perimeter of ABC, A = area of ABC
1) r = A/p
2) r = (sum of legs - hypotenuse)/2

Antony_V

r = 2A / (a+b+c)
= 25 / (10 + 5√2)
= 25 (10 − 5√2) / 50
= (10 − 5√2) / 2

A = πr²
= (10 − 5√2)²π / 4
= (37, 5 − 25√2)π
≈ 2, 145π

Nikioko

Geometry Marvels: Calculating the Incircle Area Within a Triangle

Geometry Marvels: Calculating the Incircle Area Within a Triangle

Distance between centroid and Orthocenter| geometry| @logicxonomy| #shorts

Geometry Surprise | Nine Point Circle

Math marvels: Sum of areas of infinite circles inside a right angled triangle

Why the nine point circle is tangent to the incircle?

Geometry Problem: Inscribed Circle in an Equilateral Triangle

Most Confusing Terms in Geometry #orthocentre #circumcentre #incentre #centroid #shorts #trending

Olympiad Geometry Problem #18: Altitudes, Circumcircle, Equal Segments

How to draw the Nine-Point Circle of a given Triangle (9-Point Center)

Geometry 5: KISSING Circles--Radius of Inscribed Circle

Nine Point Circle and Euler's Line

9 point circle animation | mathocube |

Nine point circle #education #shots #shorts #circle #geometry #mathematics #tricks

Olympiad Geometry Theorems | L to P

Nine Point Circle - a Geometrical Proof

Nine Point Circle | Geometry for Math Olympiad

Given a Circle Inscribed in a Triangle, Find AO+BO+CO.

GEOMETRY 20 : Nine Point Circle II

The radius of the nine point circle of the triangle whose vertices are (4,6) (0,4) (6,2) is

Puzzle: Triangle in a Square Defined by Arcs

CMI 2018 A1: Sum of areas of all the circles inside an equilateral triangle touching sides & cir...

DRAW A QUADRILATERAL AND CONSTRUCT A TRIANGLE OF SAME AREA

#Centroid #Circumcenter #Orthocenter #Incenter #Excenter #NinePointCenterOftriangle #SSCCGL

Circles inside right-angle triangles - trigonometry/geometry problems