filmov
tv
Graphical Solution of Absolute Value Inequality |x-2| + |2x+1| ≥ 3
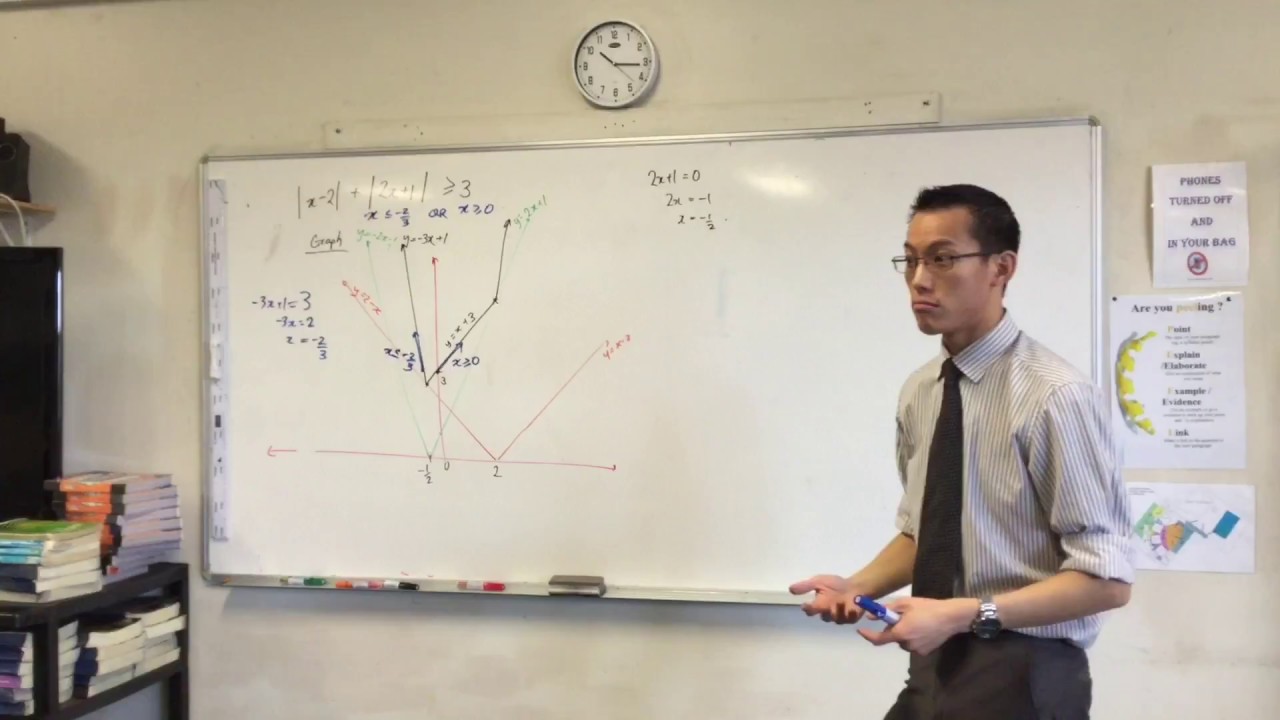
Показать описание
How To Graph Absolute Value Functions - Domain & Range
Graphs of absolute value functions | Functions and their graphs | Algebra II | Khan Academy
Graphing the absolute value function with transformations
Shifting absolute value graphs | Mathematics II | High School Math | Khan Academy
Graphing Absolute Value Functions (y=a|x-h|+k)
Absolute Value Graphs
Solving Absolute Value Equations Graphically
Sketching Harder Absolute Value Graphs
Express Inequalities as Absolute Value Function and Graph on Number Line MHF4U Test Preparation
Absolute Value Graphs (2 of 2: Adding Graphs)
Graphing an absolute value equation with transformations and a vertical stretch
Absolute Values: Defining, Calculating, and Graphing
Absolute Value Function (How to Graph)
Easiest Way to Graph Absolute Value Functions | Domain & Range | Eat Pi
Graphical solution of absolute value equations
Absolute Value Graphs (1 of 2: Understanding Shifts)
Absolute Value of a Function (pt2 quadratic) • [7.2c] Pre-Calculus 11
Graphing Absolute Value Functions (3 of 3: Reflections & non-linear curves)
Shift absolute value graphs
Graphing Absolute Value Functions - 1
how to solve an absolute value equation
Graphing a shifted and stretched absolute value function
Absolute Value Graphs (How to Graph Quickly!)
Absolute value graphs and equations
Комментарии
 0:10:54
0:10:54
 0:08:34
0:08:34
 0:02:47
0:02:47
 0:06:11
0:06:11
 0:06:52
0:06:52
 0:03:19
0:03:19
 0:02:46
0:02:46
 0:09:09
0:09:09
 0:08:36
0:08:36
 0:07:26
0:07:26
 0:03:50
0:03:50
 0:05:10
0:05:10
 0:03:44
0:03:44
 0:07:50
0:07:50
 0:03:05
0:03:05
 0:04:28
0:04:28
 0:08:54
0:08:54
 0:09:52
0:09:52
 0:04:08
0:04:08
 0:03:46
0:03:46
 0:00:24
0:00:24
 0:06:10
0:06:10
 0:01:01
0:01:01
 0:21:30
0:21:30