filmov
tv
Calculus 3: Line Integrals (14 of 44) What is a Line Integral? (y^2)dx+xdy Example 3

Показать описание
In this video I will find the line integral of (y^2)dx+xdy where C={C1,C2} using a different curve. Ex. 3
Next video in the series can be seen at:
Calculus 3: Line Integrals (14 of 44) What is a Line Integral? (y^2)dx+xdy Example 3
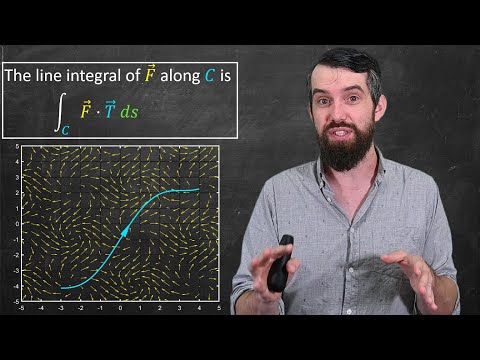
Evaluating Line Integrals
Calculus 3: Line Integrals (18 of 44) What is a Line Integral? [(y)dx+(z)dy+(x)dz] Example 6
Calculus 3: Line Integrals (Video #28) | Math with Professor V
How to Evaluate the Line Integral of a Vector Field
Introduction to the line integral | Multivariable Calculus | Khan Academy
Solve the Line Integral with the Fundamental Theorem of Line Integrals - 16.3.14 Cengage
Line Integrals Practice Problems
Calculus NCEA Level 2 in 15 hours | Part 3
What is a LINE INTEGRAL? // Big Idea, Derivation & Formula
Line Integrals of Vector Fields // Big Idea, Definition & Formula
Calculus 3 Lecture 14.2: How to Solve Double/Repeated/Iterated Integrals
Line Integrals: Full Example
Line Integrals with respect to x or y // Vector Calculus
The Fundamental Theorem for Line Integrals
Calculus 16.3 Fundamental Theorem for Line Integrals
Video 3255 - Calculus 3 - Line Integral - Spiral
Calculus 3 Lecture 14.6: How to Solve TRIPLE INTEGRALS (Along with Center of Mass and Volume)
Fundamental Theorem for Line Integrals :: Conservative Vector Field Line Integral
Path independence for line integrals | Multivariable Calculus | Khan Academy
Line Integrals of Scalar Functions (Introduction)
Line Integral Evaluation Example 1
Calculus 3: Line Integrals (7 of 44) What is a Line Integral? Using Parametric Equations
Calculus 3: Line Integrals (27 of 44) Vector Field: Evaluate a Line Integral
Комментарии
 0:07:48
0:07:48
 0:12:54
0:12:54
 0:05:03
0:05:03
 0:41:34
0:41:34
 0:06:16
0:06:16
 0:18:49
0:18:49
 0:07:23
0:07:23
 0:13:00
0:13:00
 1:08:10
1:08:10
 0:14:02
0:14:02
 0:08:40
0:08:40
 3:23:48
3:23:48
 0:05:40
0:05:40
 0:11:28
0:11:28
 0:04:16
0:04:16
 0:35:10
0:35:10
 0:07:17
0:07:17
 3:33:32
3:33:32
 0:08:09
0:08:09
 0:17:14
0:17:14
 0:25:29
0:25:29
 0:08:34
0:08:34
 0:04:48
0:04:48
 0:06:05
0:06:05