filmov
tv
Product Rule With 3 Functions - Derivatives | Calculus
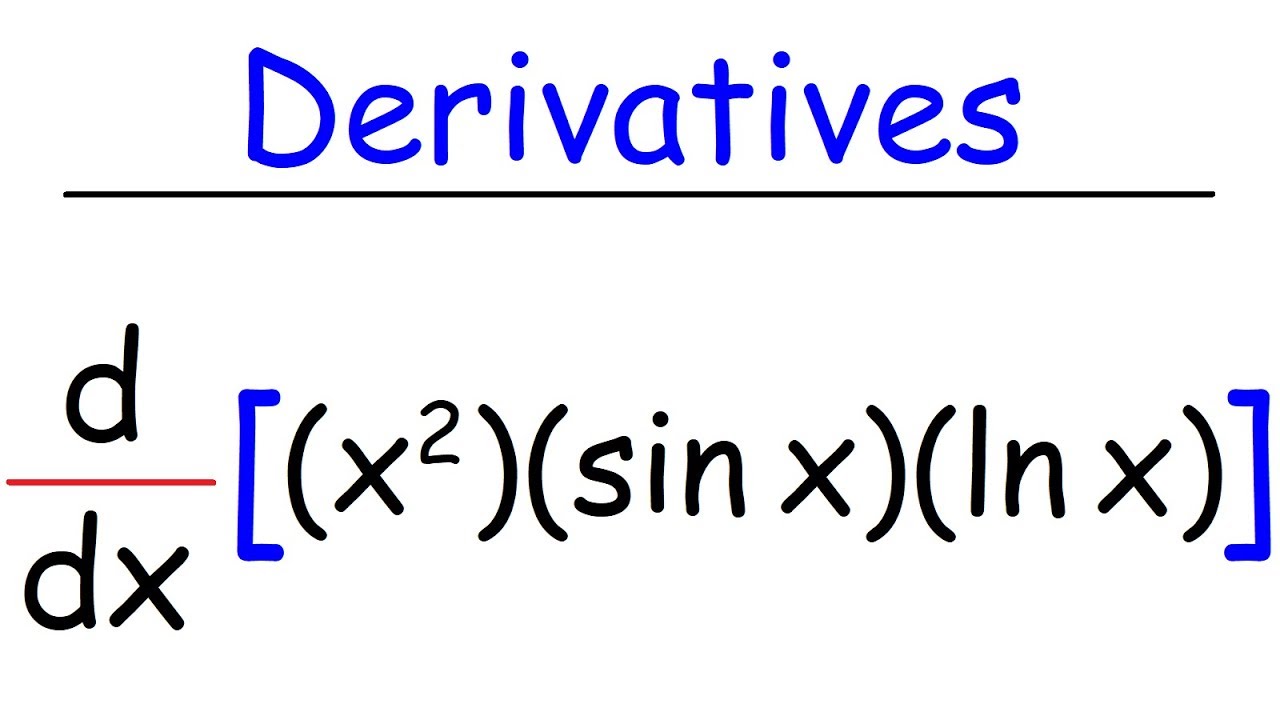
Показать описание
This calculus video tutorial explains how to find the derivative of a problem with three functions multiplied together using the triple product rule.
Equation of the Tangent Line:
Simplifying Derivatives:
Derivatives - The Product Rule - f*g:
Derivatives - Triple Product Rule - f*g*h:
Derivatives - Quadruple Product Rule - f*g*h*k:
___________________________________
Derivatives - The Quotient Rule:
Derivatives - The Chain Rule:
Chain Rule With Trig Functions:
Chain Rule - Harder Examples:
Chain Rule - Triple SQRT(x):
_________________________________
Derivatives - Composite Functions:
Implicit Differentiation:
Derivatives - Inverse Trig Functions:
Derivatives - Exponential Functions:
Derivatives - Logarithmic Functions:
___________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Derivatives - Formula Sheet:
Equation of the Tangent Line:
Simplifying Derivatives:
Derivatives - The Product Rule - f*g:
Derivatives - Triple Product Rule - f*g*h:
Derivatives - Quadruple Product Rule - f*g*h*k:
___________________________________
Derivatives - The Quotient Rule:
Derivatives - The Chain Rule:
Chain Rule With Trig Functions:
Chain Rule - Harder Examples:
Chain Rule - Triple SQRT(x):
_________________________________
Derivatives - Composite Functions:
Implicit Differentiation:
Derivatives - Inverse Trig Functions:
Derivatives - Exponential Functions:
Derivatives - Logarithmic Functions:
___________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Derivatives - Formula Sheet:
Комментарии
 0:05:08
0:05:08
 0:04:28
0:04:28
 0:03:15
0:03:15
 0:05:37
0:05:37
 0:07:23
0:07:23
 0:09:18
0:09:18
 0:07:13
0:07:13
 0:00:51
0:00:51
 1:44:34
1:44:34
 0:11:11
0:11:11
 0:03:34
0:03:34
 0:10:16
0:10:16
 0:03:32
0:03:32
 0:01:20
0:01:20
 0:04:44
0:04:44
 0:15:56
0:15:56
 0:09:26
0:09:26
 0:02:48
0:02:48
 0:04:26
0:04:26
 0:16:19
0:16:19
 0:04:34
0:04:34
 0:03:10
0:03:10
 0:17:43
0:17:43
 0:00:53
0:00:53