filmov
tv
Derivative of arctan(x^2): derivative with inverse tangent and chain rule.

Показать описание
We compute the derivative of arctan(x^2) by recognizing that this is a function composition, where x^2 is the inner function and arctan is the outer function. We need to start by taking the derivative of the inverse tangent with respect to the inner function, treating x^2 as a single variable for the derivative.
Comparing to the standard formula for the derivative of arctan(x), we simply evaluate the derivative at x^2 to obtain 1/(1+x^4). Next, the chain rule requires that we tack on the derivative of x^2 itself (the derivative of the inner function). This gives us a factor of 2x.
Finally, we simplify the derivative of arctan(x^2) to 2x/(1+x^4), and we're done!
Comparing to the standard formula for the derivative of arctan(x), we simply evaluate the derivative at x^2 to obtain 1/(1+x^4). Next, the chain rule requires that we tack on the derivative of x^2 itself (the derivative of the inner function). This gives us a factor of 2x.
Finally, we simplify the derivative of arctan(x^2) to 2x/(1+x^4), and we're done!
 0:01:05
0:01:05
 0:01:44
0:01:44
 0:01:23
0:01:23
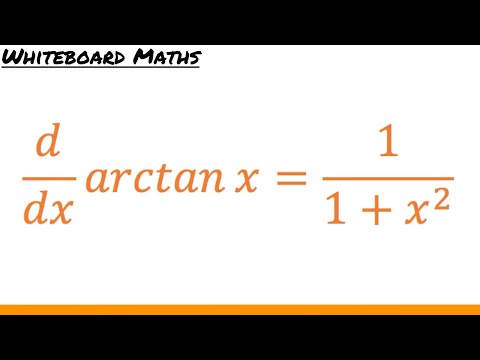 0:02:08
0:02:08
 0:00:56
0:00:56
 0:01:34
0:01:34
 0:06:19
0:06:19
 0:05:37
0:05:37
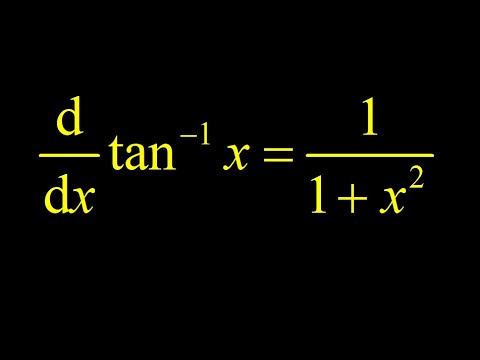 0:04:29
0:04:29
 0:00:43
0:00:43
 0:03:05
0:03:05
 0:01:29
0:01:29
 0:03:58
0:03:58
 0:06:11
0:06:11
 0:05:59
0:05:59
 0:03:11
0:03:11
 0:06:17
0:06:17
 0:03:38
0:03:38
 0:00:40
0:00:40
 0:06:47
0:06:47
 0:04:27
0:04:27
 0:05:31
0:05:31
 0:06:02
0:06:02
 0:05:23
0:05:23