filmov
tv
The Trillion Dollar FLAW in Financial Market Trading

Показать описание
Ever heard of the Black-Scholes-Merton equation? It's the bedrock of options pricing in financial markets, but what if I told you it's hiding a monstrous flaw? 🤯 Dive deep into the world of financial mathematics with me in this eye-opening video where I dissect the "trillion-dollar equation" and reveal its Achilles' heel.
Veritasium, known for its captivating science content, recently tackled this very equation, but they missed a crucial piece of the puzzle. Join me as I break down the misconceptions and uncover the hidden dangers. I'll introduce you to the reality of volatility clustering and fat-tailed distributions, concepts that could reshape your understanding of market behavior, and reveal the infamous bailout of Long-Term Capital Management's trading positions, where the brightest minds in finance were blindsided by their own models.
DISCLAIMER: This video is for educational and entertainment purposes only and does not constitute financial advice. The views expressed are my personal opinions and should not be taken as specific guidance. Investing involves risk, including the loss of principal. Always consult with a licensed financial advisor or conduct your own research before making investment decisions.
Sources and credits:
Clips modified and used under Fair Use rules, and gratefully acknowledged – please watch their video!
Clip from “House of Cards” (original BBC (UK) series) modified and used under fair use rules, and also gratefully acknowledged. Listen to Urquhart and go and watch it.
Marc Rubinstein - Washington Post article here:
Myron Scholes image:
Robert Merton image:
Massachusetts Institute of Technology, CC BY-SA 4.0
Mandelbrot photo:
Rama, CC BY-SA 2.0 FR
Coin image:
Image by Clker-Free-Vector-Images from Pixabay
Veritasium, known for its captivating science content, recently tackled this very equation, but they missed a crucial piece of the puzzle. Join me as I break down the misconceptions and uncover the hidden dangers. I'll introduce you to the reality of volatility clustering and fat-tailed distributions, concepts that could reshape your understanding of market behavior, and reveal the infamous bailout of Long-Term Capital Management's trading positions, where the brightest minds in finance were blindsided by their own models.
DISCLAIMER: This video is for educational and entertainment purposes only and does not constitute financial advice. The views expressed are my personal opinions and should not be taken as specific guidance. Investing involves risk, including the loss of principal. Always consult with a licensed financial advisor or conduct your own research before making investment decisions.
Sources and credits:
Clips modified and used under Fair Use rules, and gratefully acknowledged – please watch their video!
Clip from “House of Cards” (original BBC (UK) series) modified and used under fair use rules, and also gratefully acknowledged. Listen to Urquhart and go and watch it.
Marc Rubinstein - Washington Post article here:
Myron Scholes image:
Robert Merton image:
Massachusetts Institute of Technology, CC BY-SA 4.0
Mandelbrot photo:
Rama, CC BY-SA 2.0 FR
Coin image:
Image by Clker-Free-Vector-Images from Pixabay
Комментарии
 0:07:55
0:07:55
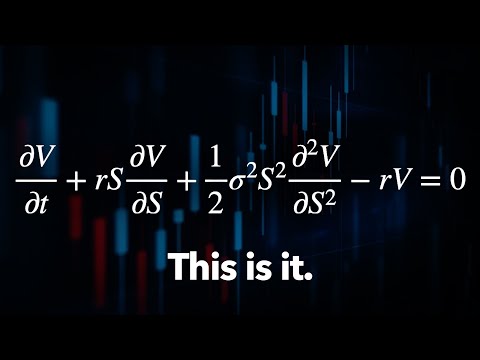 0:31:22
0:31:22
 0:00:42
0:00:42
 0:16:15
0:16:15
 0:05:56
0:05:56
 0:00:45
0:00:45
 0:00:30
0:00:30
 0:54:57
0:54:57
 0:00:50
0:00:50
 0:01:58
0:01:58
 0:00:17
0:00:17
 0:00:24
0:00:24
 0:00:11
0:00:11
 0:00:58
0:00:58
 0:00:11
0:00:11
 0:00:36
0:00:36
 0:00:17
0:00:17
 0:03:08
0:03:08
 0:00:24
0:00:24
 0:00:19
0:00:19
 0:21:11
0:21:11
 0:00:13
0:00:13
 0:00:57
0:00:57
 0:00:46
0:00:46