filmov
tv
Introduction to Continuity for Calculus

Показать описание
This video introduces the idea of discontinuity in calculus. First, we use an intuitive idea of continuity: if a function can be drawn without picking up your pen or pencil, it is continuous. For a more mathematical definition of continuity, we use the calculus definition, which is summarized in the continuity checklist. For a function to be continuous at x=a, three conditions must be fulfilled:
1. The function must be defined at x=a (a must be in the domain of f)
2. The limit must exist at x=a
3. The limit must equal f(a), that is, the value of f evaluated at a
The video then gives an example of a function with multiple discontinuities and asks us to describe why the function is continuous at each discontinuity.
ADA-compliant subtitles/captions
1. The function must be defined at x=a (a must be in the domain of f)
2. The limit must exist at x=a
3. The limit must equal f(a), that is, the value of f evaluated at a
The video then gives an example of a function with multiple discontinuities and asks us to describe why the function is continuous at each discontinuity.
ADA-compliant subtitles/captions
 0:06:39
0:06:39
 0:13:31
0:13:31
 0:14:04
0:14:04
 0:05:33
0:05:33
 0:11:15
0:11:15
 0:11:10
0:11:10
 0:10:10
0:10:10
 0:13:22
0:13:22
 0:02:10
0:02:10
 0:32:48
0:32:48
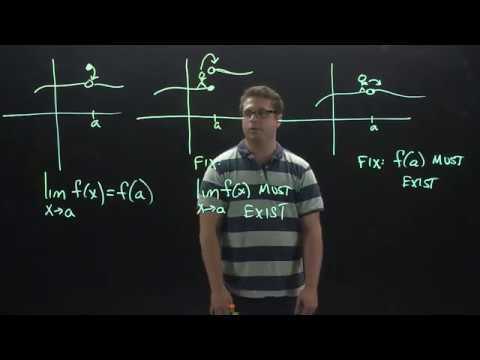 0:03:42
0:03:42
 0:11:32
0:11:32
 0:19:19
0:19:19
 0:15:01
0:15:01
 0:09:38
0:09:38
 0:07:18
0:07:18
 0:01:17
0:01:17
 0:03:45
0:03:45
 0:22:56
0:22:56
 0:06:32
0:06:32
 0:08:33
0:08:33
 0:11:14
0:11:14
 0:34:18
0:34:18
 0:25:58
0:25:58