filmov
tv
How to Get to Manifolds Naturally
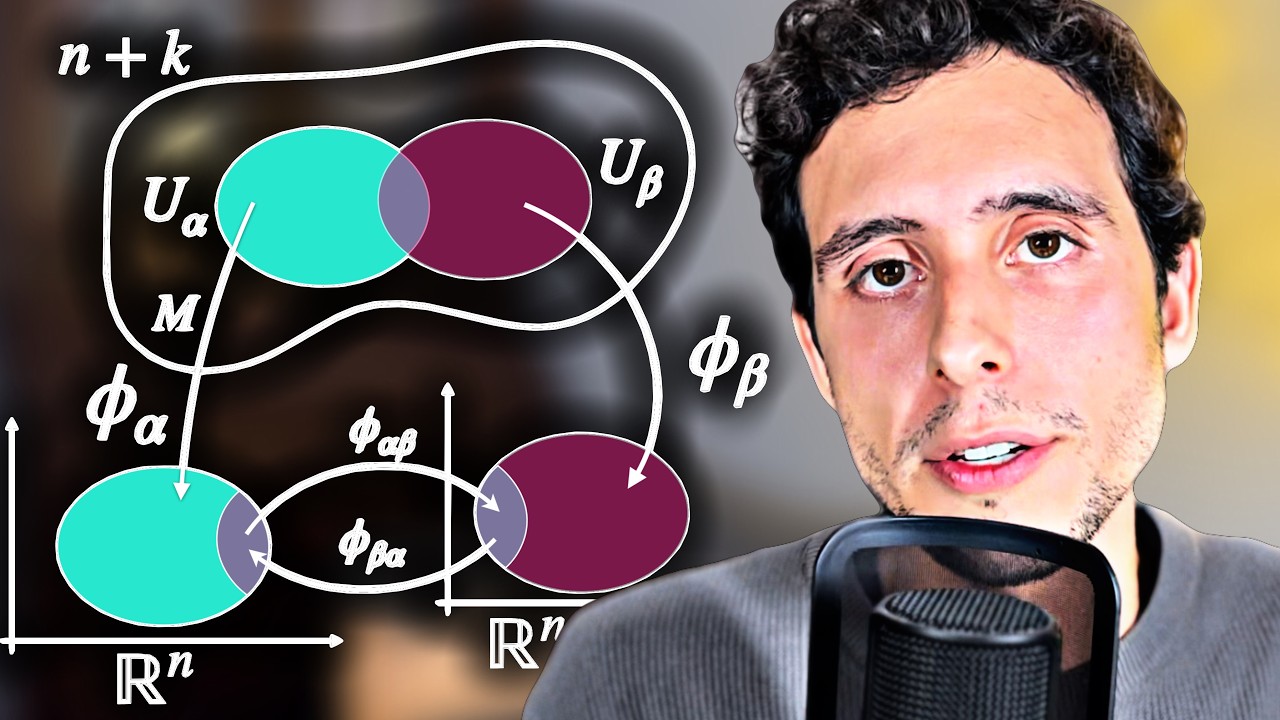
Показать описание
PDF summary link
Inspired by this book and this article:
Need a VPN?
---
Some great books for learning math or physics
😎 Become a member to have exclusive access:
🥹 Consider supporting us on Patreon:
Inspired by this book and this article:
Need a VPN?
---
Some great books for learning math or physics
😎 Become a member to have exclusive access:
🥹 Consider supporting us on Patreon:
How to Get to Manifolds Naturally
How to get started selling MANIFOLDS
Satisfactory: Manifold vs Load Balancing for Belts + Tutorial
Manifolds Explained in 5 Levels of Difficulty
How to self study pure math - a step-by-step guide
The TRUTH on Intake Manifolds 😳 #shorts
Headers vs. Manifolds - Do they change your exhaust note?
Are Headers Worth It?
#333-Pro Flo 4 Install. It's good. VERY good.
How Do You Choose? 🤷♂️ Exhaust Manifolds vs. Headers, EXPLAINED
EQUAL LENGTH tubular vs. LOG manifolds (headers) - SCAVENGING and EXHAUST BACK PRESSURE EXPLAINED
Exhaust Manifolds vs. Headers: How much power will you gain? #headers #exhaust
Manifolds #1 - Introducing Manifolds
Lecture 2B: Introduction to Manifolds (Discrete Differential Geometry)
Headers vs Manifolds - Summit Racing 101
BREAKING NEWS. The Plastic Manifolds Chrysler Use Is Not The Enemy. Here's why.
Turbo Your Car - Choosing an Exhaust Manifold
How to Build Manifolds the Overflow Method [Satisfactory Basics Guide]
What are plumbing manifolds
Neural manifolds - The Geometry of Behaviour
Smells, or Ticking? Diagnose a Car or Truck Exhaust Manifold Leak
All 7 LS Intake Manifolds Explained
Manifolds
Speedway Tech Talk - Tips for Selecting an Intake Manifold
Комментарии
 0:08:46
0:08:46
 0:31:41
0:31:41
 0:06:23
0:06:23
 0:08:24
0:08:24
 0:09:53
0:09:53
 0:00:38
0:00:38
 0:00:43
0:00:43
 0:11:53
0:11:53
 0:46:04
0:46:04
 0:06:09
0:06:09
 0:17:43
0:17:43
 0:00:49
0:00:49
 0:12:37
0:12:37
 0:47:44
0:47:44
 0:04:04
0:04:04
 0:01:00
0:01:00
 0:12:47
0:12:47
 0:20:03
0:20:03
 0:02:54
0:02:54
 0:23:17
0:23:17
 0:09:07
0:09:07
 0:00:59
0:00:59
 0:13:46
0:13:46
 0:03:37
0:03:37