filmov
tv
Find the blue shaded area | Math Olympiad Geometry Problem | Important Geometry and Algebra Skills

Показать описание
Find the blue shaded area | Math Olympiad Geometry Problem | Important Geometry and Algebra Skills
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
Sambasivam Sathyamoorthy
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Grace Cooper
Nicholas Garcia
Ben Stone
Karlo Karbs
Debashis Kesh
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
Sambasivam Sathyamoorthy
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Grace Cooper
Nicholas Garcia
Ben Stone
Karlo Karbs
Debashis Kesh
Find the blue shaded area | Geometry Problem | Important Geometry Skills explained
Find the blue shaded area | Geometry Problem | Important Geometry Skills Explained
Find the blue shaded area | Geometry Problem | Important Geometry and Algebra Skills Explained
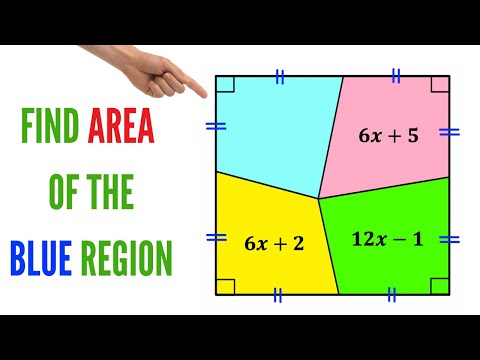
Find the blue shaded area of the square | A Nice Geometry Problem
Geometry Problem: The Value of the Blue Shaded Area?
Calculate the Blue Shaded Area. Geometry problem/
Find the blue shaded area | Given a rectangle and a square | Important Geometry Skills Explained
Find the blue shaded area | Geometry Problem | Important Geometry Skills Explained
BeckerArt Sunday Watercolor Demo with David... Alan's Harley
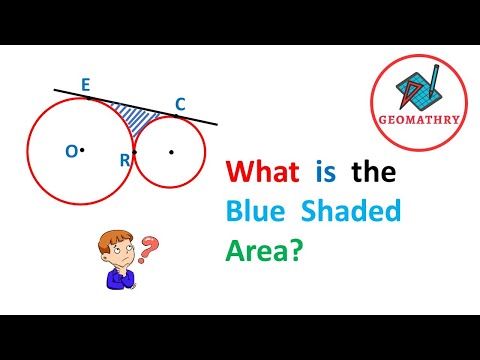
Find the blue shaded area | Math Olympiad Geometry Problem | Important Geometry and Algebra Skills
Find the Area of the Blue Shaded Region | Step-by-Step Tutorial
Find the blue shaded area | Geometry Problem | 2 Different Methods to Solve
Find the blue shaded area | Geometry Problem | 2 Different Methods | Very Important Geometry Skills
Can You Find The Blue Shaded Area | Improve your Geometry Skill
Can you find the area of the Blue shaded region? | (Important Geometry skills explained) #math
Find The Area of The Blue Shaded Region in The Square | Geometry | Math | 2 Methods
Find The Blue Shaded Area in The Quadrilateral | Geometry | Math
Find The Blue Shaded Area | 3 squares inside a triangle | Important Geometry Skills Explained
Find the blue shaded area | Geometry Problem | Important Geometry and Algebra Skills Explained
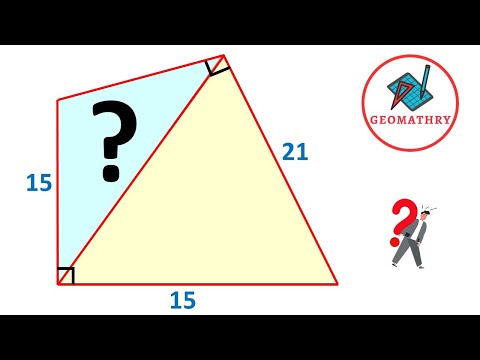
Find the blue shaded area of the triangle | A Nice Geometry Problem | 3 Different Methods to Solve
Find the blue shaded area | Semicircle inside a quarter circle | Calculus | Area under the curve
How to Find The Blue Shaded Area Using Euclid Theorem | Improve your Geometry Skill
Calculate the blue shaded area | Geometry Problem | 2 Different Methods
Find the blue shaded area | Given a semicircle inside a quarter circle | Geometry Problem | 2 Method
Комментарии
 0:09:52
0:09:52
 0:08:07
0:08:07
 0:15:12
0:15:12
 0:09:56
0:09:56
 0:09:31
0:09:31
 0:02:54
0:02:54
 0:10:04
0:10:04
 0:07:47
0:07:47
 1:03:15
1:03:15
 0:22:38
0:22:38
 0:06:21
0:06:21
 0:13:55
0:13:55
 0:20:10
0:20:10
 0:04:55
0:04:55
 0:08:02
0:08:02
 0:08:01
0:08:01
 0:06:23
0:06:23
 0:09:10
0:09:10
 0:07:09
0:07:09
 0:15:19
0:15:19
 0:20:44
0:20:44
 0:04:34
0:04:34
 0:13:54
0:13:54
 0:13:24
0:13:24