Supremum of a set

Supremum of a set

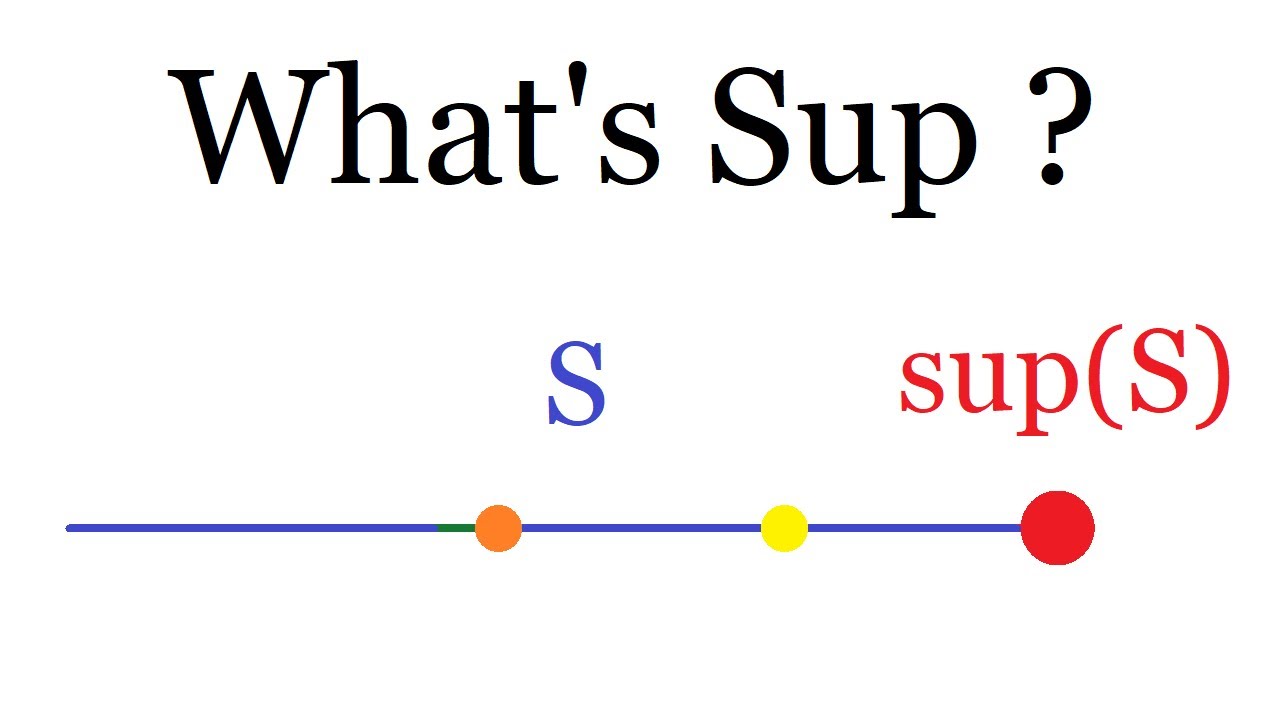
In this video, which is the most important video of the chapter, I define the supremum of a set of real numbers. It is like a maximum, except that it always exists, and will be super useful in the rest of our analysis adventure.

[pedropeixoto]

Your definition is clearer than how most real analysis books put it. Not that I have read more than a few books on the subject, ..., but still.

[jupitersolarsystem]

Thank you for the clear explanation. I am a self-learner so this lectures help a lot when I do not understand a concept from textbooks.

[CliffStamp]

That is an elegant way to define something like a general maximum for a set.

[bertrandspuzzle]

Where we're going, we won't need bounds.

[valelopez]

please don't change. love this content

[Kdd]

1:32
"SOUP"??
IN THE SUBTITLES LOLLLL

[LucaIlarioCarbonini]

Definetively something I was looking for! Thanks!

[justpassingby]

I have a question sir : In this video you stated if M1 < 4 and S1 > M1 then 4 has to be a sup. Doesn't that mean 5 is also a sup(least upper bound) in that definition?
Thanks in advance.

[moshadj]

This works for any ordered set as well. But not all ordered sets have the Least Upper Bound property (the property that a bounded, non-empty set has a supremum in the containing ordered set). Consider the following subset of the rationals, the rationals who's square is lesser equal to 2. Clearly from high school math we know the sup of this set would be sqrt(2), but also from that same math class we know sqrt(2) is irrational and in particular there is no sup in the rationals even though the set is clearly non-empty and bounded.

[IoT_]

I was wondering : does it work for field of the rational numbers? We could divide at half the interval infinitely many times as well but I have a feeling that it can messed up because Rationals are countable.

[raydencreed]

If, for a given set, we define a new set of upper bounds, could we define the supremum as the minimum of that set instead?

[omaymaouhadi]

Thaaanks a lot this is such as a great explication!!!

[tomkerruish]

How do you intend to prove this as a theorem? Are you going to construct the reals as Dedekind cuts or Cauchy sequences of the rationals, or perhaps in some other fashion?

[foreachepsilon]

Why might it be reductive to say “supremum is a maximum with a built-in limit”?

[xavierplatiau]

1:00 You were right to say « non empty bounded subset of R »
For exemple R which is not bounded has no sup.
So I wonder, will you be talking about the extended real line in which every subset has an inf and a sup one day? That would be amazing !

[SartajKhan-jgnz]

Say we have a set S, and X is less or equal to the Sup(S). If we can show that, if Y is an element of S greater than X, X=Y then does that imply X=Y=sup(S)?

[joefuentes]

Why isnt supremeum defined like for all elements x in S then x <= M?

[muyangyan]

This was made on my birthday lol. Thanks for the tutorial

[sanderneckebroeck]

Best joke I heard for supremum... Will do it on the exam! :)

[GabrielRamirez-sdfz]

Dr.Peyam could you explain some theory of Gauss Eliminitation please. From Perú 😃