filmov
tv
Solving 8^x+2^x=130 | An Exponential Equation
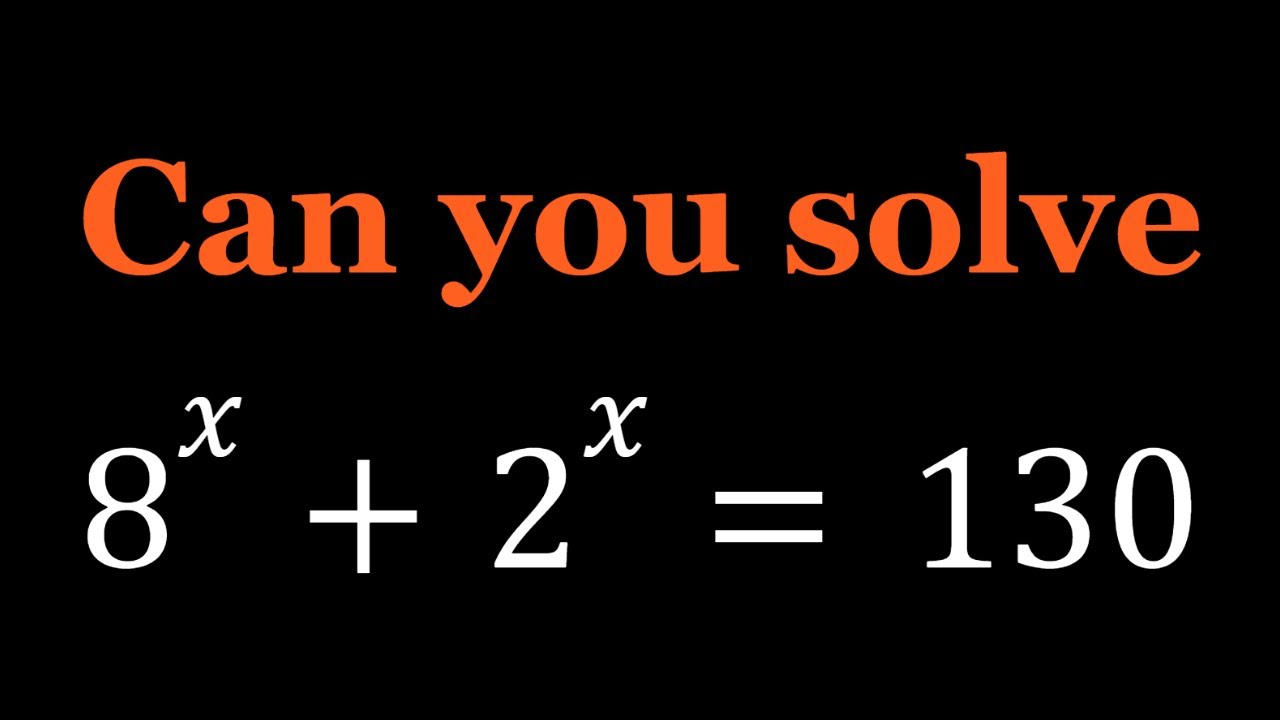
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving 8^x+2^x=130 | An Exponential Equation
Exponential Equation | 8^x + 2^x = 130
How to solve 8^x +2^x =130 | A fine Olympiad math problem | Mental Math
Master Equation Solving:Solve 8^x + 2^x = 130.Step-by-Step Tutorial for Exponential Equations.in sec
A Nice Olympiad Exponential Equation | 8^x+2^x=130 | Solve for x. @freemathsvideos
A Wonderful Exponential Math Equation Solving. Olympiad Mathematics , 8^x+2^x=130
A Nice Olympiad Exponential Problem | 8^x + 2^x = 130|
IF 8^x+2^x=130 Then X=? | Entrance Exam Question
Solving 8^x+2^x=130 | An Exponential Equation | Math Olympiad
Equation : 2^x + 8^x =130 - Olympiad mathematics
𝑀𝑎𝑠𝑡𝑒𝑟𝑖𝑛𝑔 𝐸𝑥𝑝𝑜𝑛𝑒𝑛𝑡𝑖𝑎𝑙 𝐸𝑞𝑢𝑎𝑡𝑖𝑜𝑛𝑠: 𝑆𝑜𝑙𝑣𝑖𝑛𝑔 8^𝑥 + 2^𝑥 = 130...
Hard Math Olympiad Problem. How to solve this beautiful exponential equation
A Nice Olympiad Exponential Problem | 8^x + 2^x = 130
A nice mathematics olympiad problem | Exponential equation | Solve for x | 8^x+2^x = 130 | Doubtlet
Mathematics Olympiad@ How to solve Exponential Problem i.e 8^x +2^x =130
8^x + 2^x = 130. Many Failed to solve this nice UK Math Olympiad Problem! Can you do it?
Nice Math Olympiad Exponential Problem | You Should Be Able To Solve This | How to Solve 8^x+2^x=130
Mexico | A wonderful maths olympiad question | 8^x +2^x =130.
A Nice Olympiad Exponential Problem | 8^x + 2^x = 130 | MAA AMC
How to solve exponential equation 8^x+2^x=130 |An Exponential Equation
How to Solve 8^x + 2^x = 130 | Math Learning and Mathematicals Easy Tricks | Step-by-step Algebra
Can you solve this? | Exponential Equation | Algebra Problem.
Math Olympiad 8^x+2^x=130 | Olympiad Mathematics | Best Trick...
Mexico - A Nice Math Olympiad Exponential Problem
Комментарии
 0:08:14
0:08:14
 0:01:00
0:01:00
 0:02:01
0:02:01
 0:03:17
0:03:17
 0:13:23
0:13:23
 0:07:47
0:07:47
 0:08:26
0:08:26
 0:04:11
0:04:11
 0:05:21
0:05:21
 0:03:02
0:03:02
 0:09:45
0:09:45
 0:05:33
0:05:33
 0:19:24
0:19:24
 0:07:52
0:07:52
 0:12:50
0:12:50
 0:09:12
0:09:12
 0:08:01
0:08:01
 0:07:31
0:07:31
 0:04:21
0:04:21
 0:14:49
0:14:49
 0:04:53
0:04:53
 0:03:33
0:03:33
 0:08:14
0:08:14
 0:08:36
0:08:36