filmov
tv
More homology computations | Algebraic Topology | NJ Wildberger
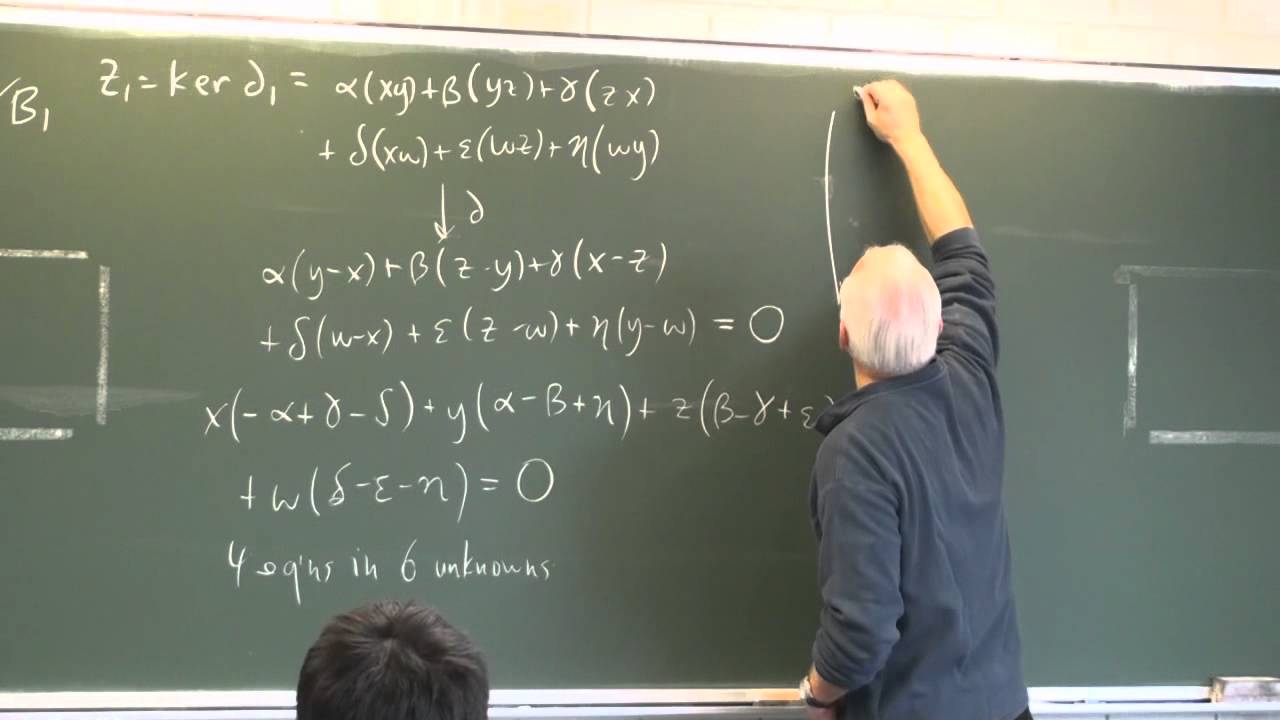
Показать описание
In our last lecture, we introduced homology explicitly in the very simple cases of the circle and disk. In this lecture we tackle the 2-sphere. First we compute the homology using the model of a tetrahedron: four 2-dimensional faces, but no 3-dim solid. This illustrates how linear algebra naturally arises in this kind of problem.
We then provide a much simpler alternative calculation using the more flexible framework of semi-simplicial complexes, or delta-complexes, where only two triangular faces are needed, and the calculation is much simplified, however still giving the same final result (which by the way is that H_0 (S^2)=Z, H_1 (S^2)=0 and H_2 (S^2)=Z, with all higher homology groups being 0.
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
We then provide a much simpler alternative calculation using the more flexible framework of semi-simplicial complexes, or delta-complexes, where only two triangular faces are needed, and the calculation is much simplified, however still giving the same final result (which by the way is that H_0 (S^2)=Z, H_1 (S^2)=0 and H_2 (S^2)=Z, with all higher homology groups being 0.
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
More homology computations | Algebraic Topology | NJ Wildberger
An introduction to homology (cont.) | Algebraic Topology | NJ Wildberger
Algebraic Topology - Lecture 12 - Computing Homology
Smith Normal Form and Homology computation [Weiyi Xiao]
Computing homology groups | Algebraic Topology | NJ Wildberger
TRHW02 | Dominic Joyce | Vertex algebra and Lie algebra structures on the homology of moduli spaces
Algebraic Topology: L10, homology functor, 9-27-16, part 1
An introduction to homology | Algebraic Topology | NJ Wildberger
Algebraic Topology: L12, homology, 10-4-16, part 1
Very basic homology calculations
How to solve a circuit using algebraic topology (intro to homology theory)
Evgeny Gorski: Algebra, Geometry and combinatorics of link homology
Hochschild (co)homology and geometric regularity - Andrea Solotar
Algebraic Topology 10: Simplicial Homology
Relative homology
The Idea of Homology
Algebraic Topology: L9, Singular Homology, 9-27-16, part 1
Algebraic Topology - Lecture 11 - Homology of Simplicial Complexes
MATH 496/696 Example persistent homology calculation
Delta complexes, Betti numbers and torsion | Algebraic Topology | NJ Wildberger
Andrew J. Blumberg: 'Abstract homotopy theory for topological data analysis'
Lori Ziegelmeier: Minimal Cycle Representatives in Persistent Homology using Linear Programming
The First Homology Group of the Projective Plane
You Could Have Invented Homology, Part 1: Topology | Boarbarktree
Комментарии
 0:42:55
0:42:55
 0:41:25
0:41:25
 2:23:35
2:23:35
 0:12:13
0:12:13
 0:41:07
0:41:07
 1:08:50
1:08:50
 0:59:51
0:59:51
 0:46:57
0:46:57
 0:59:51
0:59:51
 0:24:50
0:24:50
 0:29:18
0:29:18
 1:10:50
1:10:50
 1:01:40
1:01:40
 1:26:36
1:26:36
 0:14:38
0:14:38
 0:08:25
0:08:25
 0:59:51
0:59:51
 1:53:22
1:53:22
 0:18:56
0:18:56
 0:48:17
0:48:17
 1:00:30
1:00:30
 0:50:08
0:50:08
 0:08:56
0:08:56
 0:11:11
0:11:11