filmov
tv
Computing homology groups | Algebraic Topology | NJ Wildberger
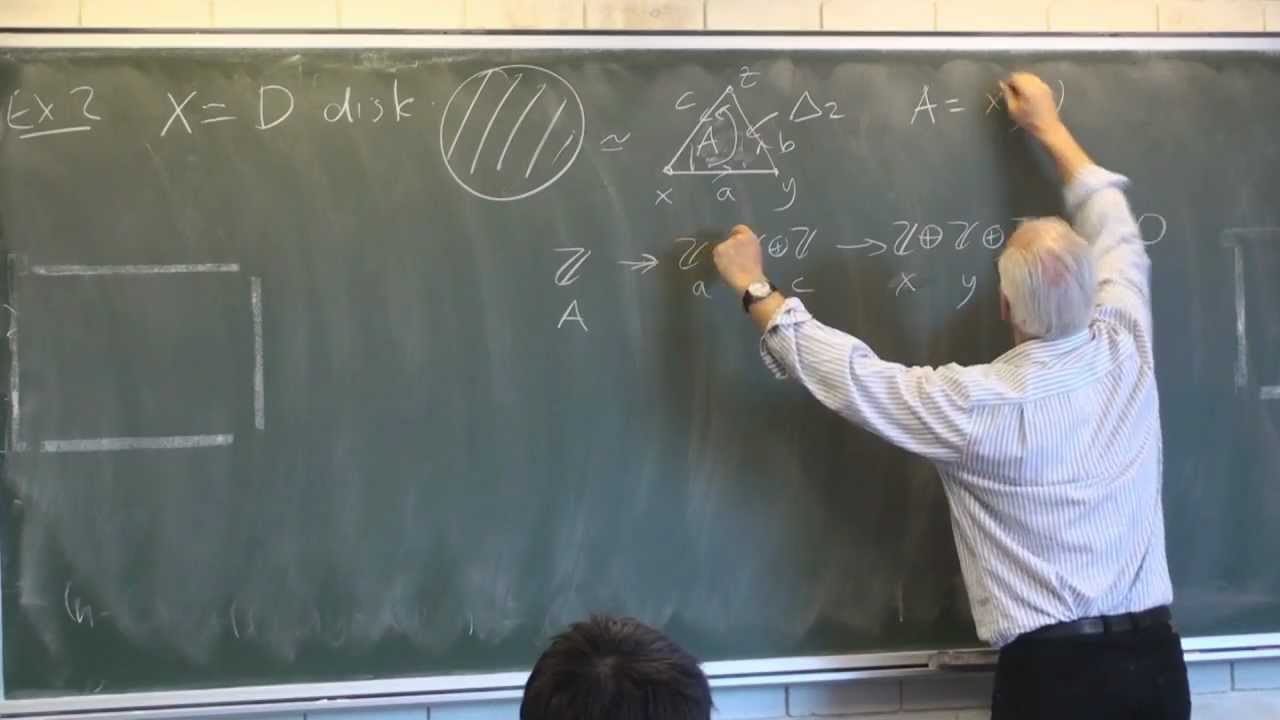
Показать описание
The definition of the homology groups H_n(X) of a space X, say a simplicial complex, is quite abstract: we consider the complex of abelian groups generated by vertices, edges, 2-dim faces etc, then define boundary maps between them, then take the quotient of kernels mod boundaries at each stage, or dimension.
To make this more understandable, we give in this lecture an in-depth look at some examples. Here we start with the simplest ones: the circle and the disk. For each space it is necessary to look at each dimension separately. The 0-th homology group H_0(X) measures the connectivity of the space X, for a connected space it is the infinite cyclic group Z of the integers. The first homology group H_1 measures the number of independent non-trivial loops in the space (roughly). The second homology group H_2 measures the number of independent non-trivial 2-dim holes in the space, and so on.
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
To make this more understandable, we give in this lecture an in-depth look at some examples. Here we start with the simplest ones: the circle and the disk. For each space it is necessary to look at each dimension separately. The 0-th homology group H_0(X) measures the connectivity of the space X, for a connected space it is the infinite cyclic group Z of the integers. The first homology group H_1 measures the number of independent non-trivial loops in the space (roughly). The second homology group H_2 measures the number of independent non-trivial 2-dim holes in the space, and so on.
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
Комментарии
 0:41:07
0:41:07
 0:41:25
0:41:25
 1:26:36
1:26:36
 0:23:40
0:23:40
 0:10:53
0:10:53
 0:17:45
0:17:45
 2:23:35
2:23:35
 0:24:15
0:24:15
 0:03:12
0:03:12
 0:13:18
0:13:18
 0:29:04
0:29:04
 0:02:17
0:02:17
 0:24:50
0:24:50
 0:15:59
0:15:59
 0:48:08
0:48:08
 0:29:18
0:29:18
 0:46:57
0:46:57
 0:04:09
0:04:09
 0:25:26
0:25:26
 0:11:11
0:11:11
 0:29:49
0:29:49
 0:15:53
0:15:53
 1:53:22
1:53:22
 0:50:08
0:50:08