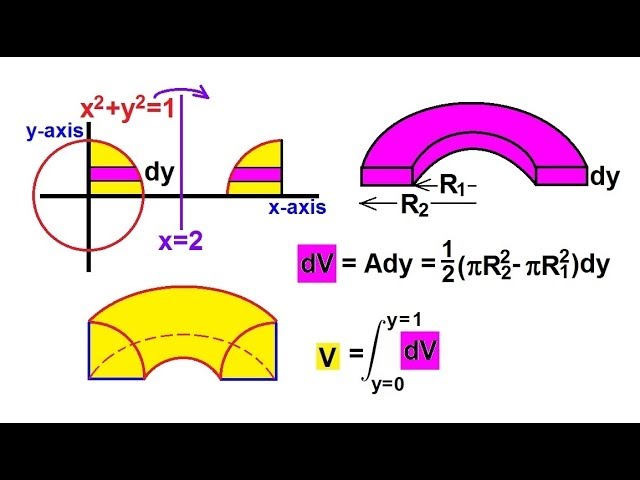
Calculus - Integration: Volume by Rotating an Area (7 of 10) Ex. 7: x^2+y^2=1, x-, y-axis About x=2.

In this video I will find the volume bounded by x^2+y^2=1, x-axis, y-axis about x=2.

[wcruzwc]

Besides the end substitution for pi, that instead of pi/2- he squared and it became pi/4, the brilliant part was substituting for y=sin (theta) and then using the trigonometric identity.

[richardrigling]

You realize that by trying to combine steps, and then finding errors, is a great way to emphasize the necessity of tedious, stepwise derivations. No doubt this is purely coincidental, and not part of your plan for this lesson. Nice

[alfredoryelcius]

sir u were mistaken at the last part. should have been phi^2/2 instead of phi^2/4 because it is phi times phi/2

[erkansamhal]

The result may be wrong..! Think a full toroid and try to find the whole volume of it. R=1, so the area is (Pi) and multiply it by the perimeter to get the volume. The result will be (Pi)*(2*Pi*2)=4*(Pi)^2. In this example, there is a quarter toroid which volume is being calculated for. So, the requested volume should be (Pi)^2.

[ThilebanTheEngineer]

if it's a circle and bounded by x axis and y axis. isn't all 4 quadrants are bound inside?. confused. 😐

[MasayoMusic]

This was a tough problem. I didnt' know you could just substitute y for a trig function.

[ikeofili]

I used a dx instead of a dy and still got the same answer. I wouldn't have thought to try that (less conventional) method if I didn't watch the previous video on this series so thank you!!

[umermubeen]

dear sir there is a mistake at 11:35 of the video ; the cos(theta) should be used instead of [1/2(1+cos(theta))]

[danialm.s]

Dear Sir,
Many Thanks for this wonderful video. It was as great as always.
I am just wondering what if the circle equation was x^2+y^2= 9...Then the limits of integration would have been 0 and 3. In that case could we still use trig substitution? If not, would it be still possible to calculate the volume?

[anamir]

Sir, Just one question. How do you know how to 'slice' the shape. I mean, how do we know how to do it. Any tips or tricks?

[dolomix]

Hello Professor, do you think it was also possible to calculte dV=πR(h)dx --> dV=π(2-x)( √(i-x^2))dx , using the same method of the previous lecture? (i tried but i came up with a different result =π2/3 ) Thank you, Best Regards

[wcruzwc]

Answer is wrong. Answer you've been [pi(pi/2 - 1/3)] not [pi(pi/4 - 1/3)]