filmov
tv
What's the Volume of a Donut? Calculus
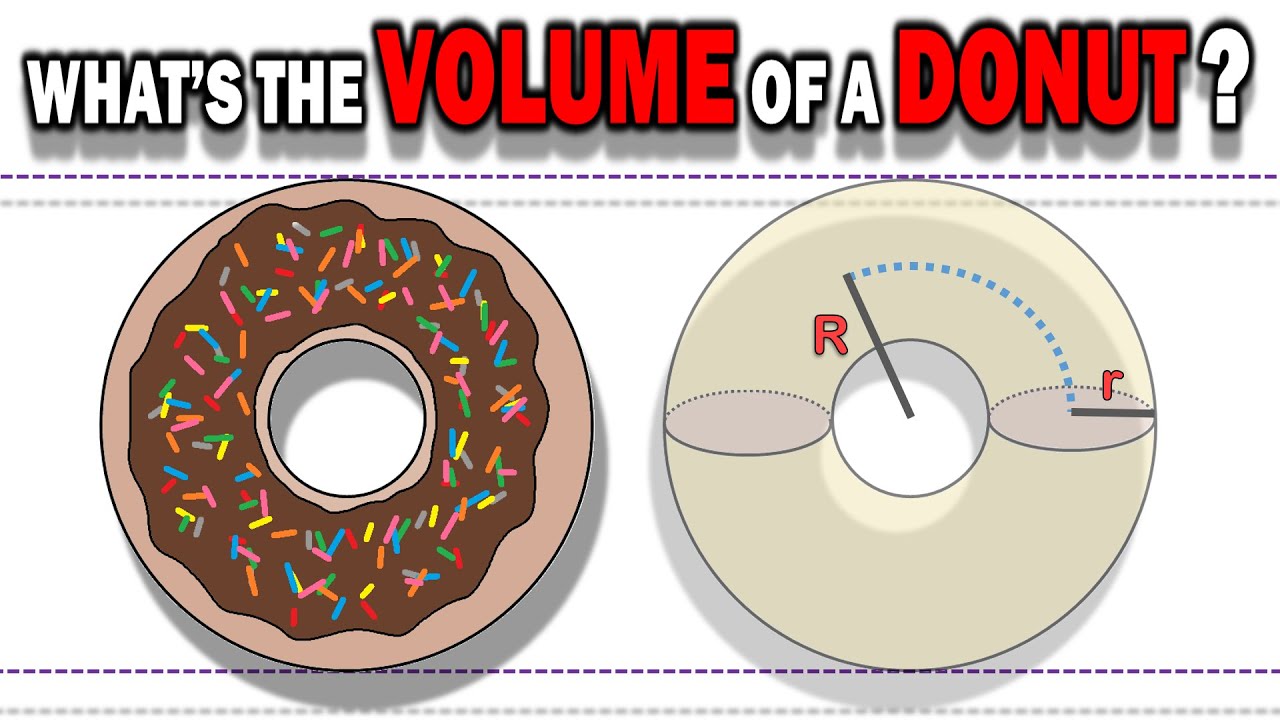
Показать описание
What is Volume in Math? Calculate Volume of Rectangular Prisms & Cubes w/ Units - [5-8-13]
Math Antics - Volume
Volume of Rectangular Prisms | Math with Mr. J
Finding Volume with Unit Cubes | How to Find Volume
How To Calculate The Volume Of A Cube Or Box - Formula For The Volume Of A Cube Or Box Explained
Volume of a Cube
Volume
Visualizing the Volume of a Sphere Formula | Deriving the Algebraic Formula With Animations
Overall M&A Volumes In Election Year Is In-line With Past Year Trends: JPMorgan | CNBC TV18
The Volume of a Sphere - Numberphile
What is Volume of a Cylinder? - [8-8-7]
What is Volume? | What is Surface Area? | Don't Memorise
Volume of a Sphere | MathHelp.com
Volume Song | Measuring Volume For Kids | 4th Grade - 5th Grade
How to Find the Volume of a Cylinder | Math with Mr. J
Volume of a Sphere
How to find the volume of a cube
Volume of Liquids
Volume of a Cylinder and Surface Area of a Cylinder
Volume and Capacity
Volume of a Cylinder
Measuring Volume by Counting Unit Cubes
Volume of a Pyramid
Volume of a Cylinder | MathHelp.com
Комментарии
 0:12:03
0:12:03
 0:12:36
0:12:36
 0:05:47
0:05:47
 0:05:36
0:05:36
 0:00:54
0:00:54
 0:01:24
0:01:24
 0:12:11
0:12:11
 0:03:12
0:03:12
 0:11:56
0:11:56
 0:04:14
0:04:14
 0:11:38
0:11:38
 0:02:44
0:02:44
 0:01:57
0:01:57
 0:02:12
0:02:12
 0:03:57
0:03:57
 0:01:27
0:01:27
 0:01:26
0:01:26
 0:01:54
0:01:54
 0:11:14
0:11:14
 0:01:42
0:01:42
 0:01:43
0:01:43
 0:03:26
0:03:26
 0:01:50
0:01:50
 0:02:03
0:02:03