filmov
tv
A Homemade Exponential Equation | 3^{x^2}9^x=27^{{sqrt(x)}

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving A Homemade Exponential Equation
A Home-made Exponential Equation
A Homemade Exponential Equation | Problem 297
A Homemade Exponential Equation
How To Solve A Homemade Exponential Equation
A Homemade Exponential Equation
A Homemade Exponential Equation
Solving A Homemade Exponential Equation
A Nice Homemade Exponential Equation
A Homemade Exponential Equation | 3^{x^2}9^x=27^{{sqrt(x)}
Solving A Homemade Exponential Equation
An Interesting Homemade Exponential Equation
A Homemade Exponential Equation | SyberMath
A Homemade Exponential Equation Solved in Three Ways
A Homemade Exponential Equation
Let's Solve A Homemade Exponential Equation 😉
Let's Solve A Homemade Exponential Equation | Problem 239
Solving a Nice Homemade Exponential Equation
How To Solve A Homemade Exponential Equation
A Homemade Exponential Equation, x^x=2^{1/x}
A Homemade Exponential Log Equation
A Very Exponential Equation (Homemade!)
Solving A Homemade Eulerian Exponential Equation
Solving x^(1/x)=sqrt(2), a Homemade Exponential Equation
Комментарии
 0:08:46
0:08:46
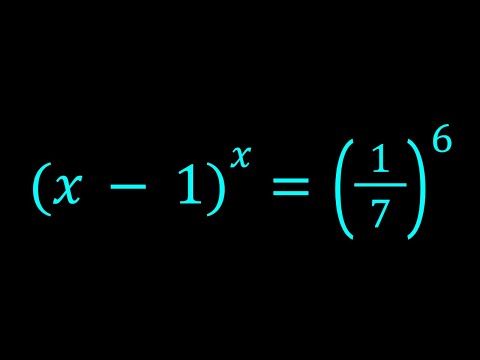 0:05:06
0:05:06
 0:07:51
0:07:51
 0:10:08
0:10:08
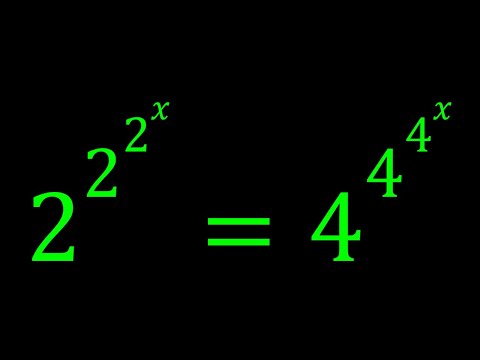 0:12:59
0:12:59
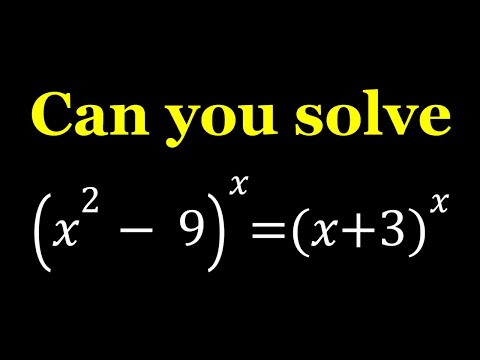 0:08:30
0:08:30
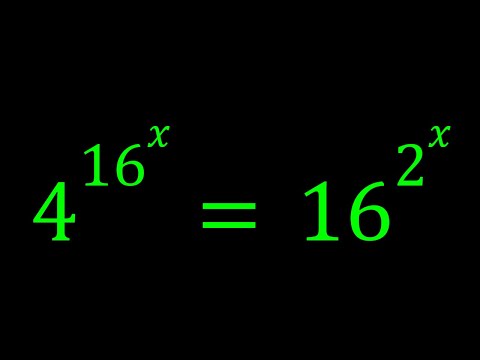 0:04:51
0:04:51
 0:09:01
0:09:01
 0:05:31
0:05:31
 0:08:59
0:08:59
 0:08:48
0:08:48
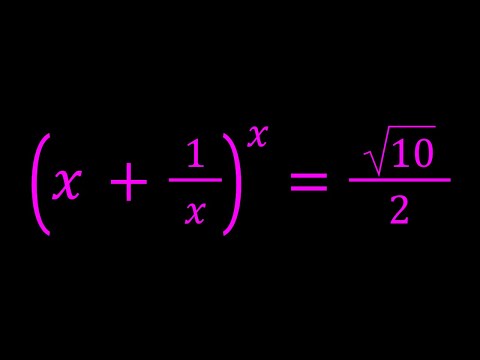 0:08:55
0:08:55
 0:07:39
0:07:39
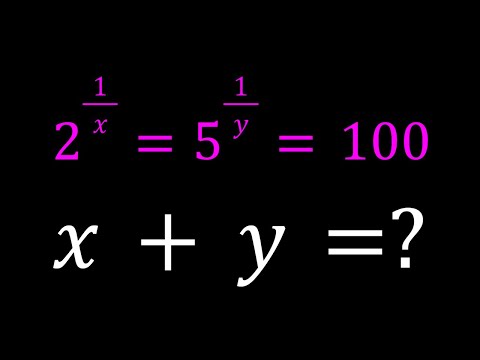 0:09:15
0:09:15
 0:10:47
0:10:47
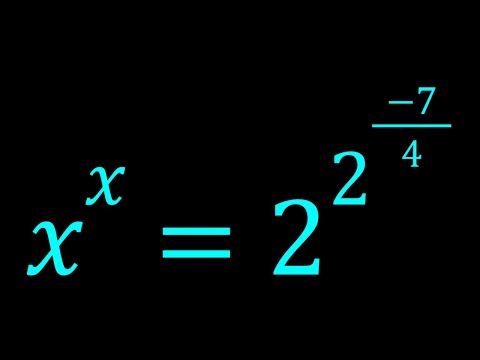 0:08:56
0:08:56
 0:09:18
0:09:18
 0:11:52
0:11:52
 0:10:41
0:10:41
 0:10:39
0:10:39
 0:09:14
0:09:14
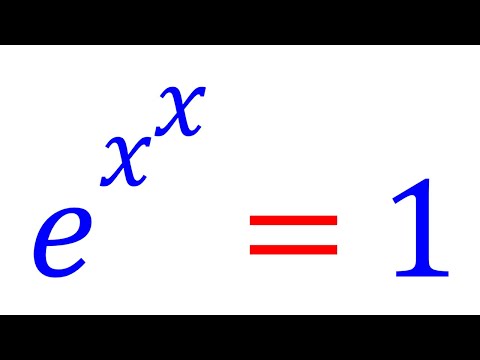 0:10:20
0:10:20
 0:09:18
0:09:18
 0:09:05
0:09:05