The Fundamental Theorem of Arithmetic

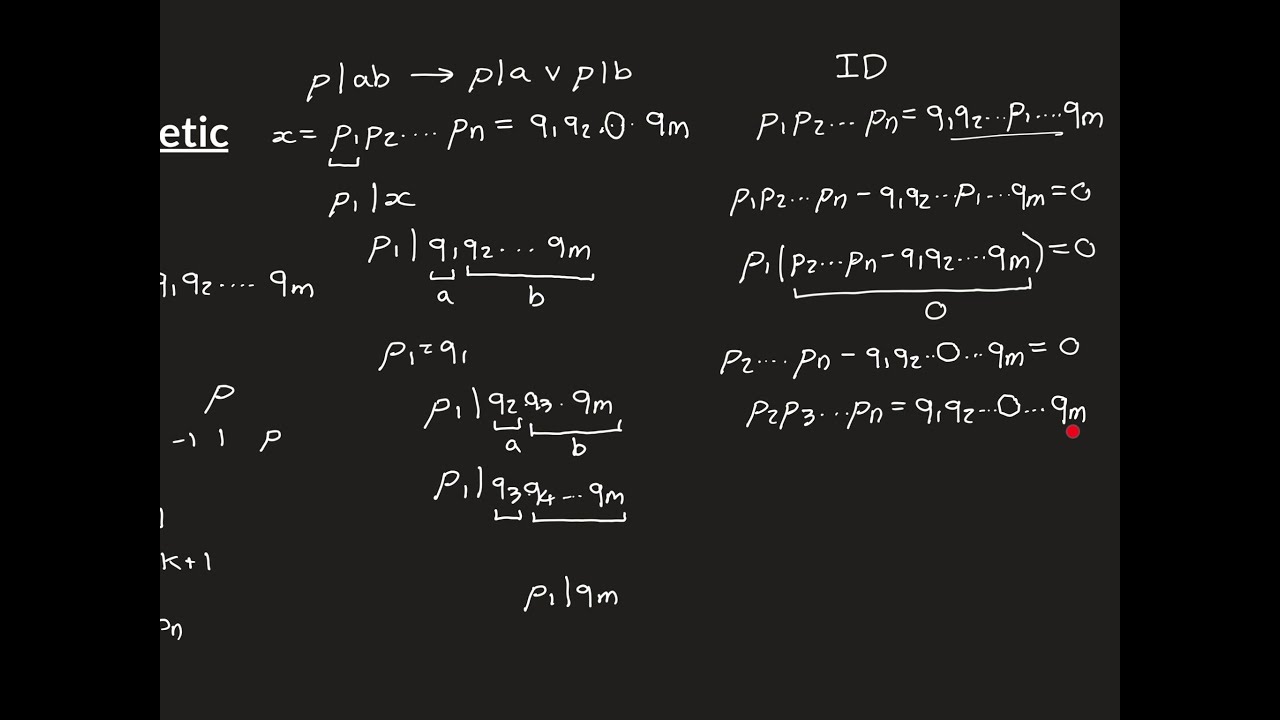
preview_player
Показать описание
The fundamental theorem of arithmetic is also called the prime factorisation theorem and the unique factorisation theorem.

It states that for any positive integer greater than or equal to 2, that the number is either prime itself or it can be written as the product of prime numbers.

This product of primes is known as the prime factorisation of the number.

The theorem goes further and says that not only does the prime factorisation exist but that it is also unique up to rearrangement of the order that the primes appear in the product.

In this video we prove this. The proof relies on Euclid’s Lemma. So please be familiar with this before watching.
  1. Elliot Nicholson
  2. The fundamental theorem of arithmetic
  3. fundamental theorem of arithmetic
  4. The Fundamental Theorem of Arithmetic
  5. the fundamental theorem of arithmetic
  6. fundamental theorem of arithmetic proof
Рекомендации по теме
The Fundamental Theorem 0:05:17

The Fundamental Theorem of Arithmetic

Proof of The 0:02:18

Proof of The Fundamental Theorem of Arithmetic

Number Theory | 0:13:09

Number Theory | Fundamental Theorem of Arithmetic

(Abstract Algebra 1) 0:05:04

(Abstract Algebra 1) Fundamental Theorem of Arithmetic

The Fundamental Theorem 0:00:15

The Fundamental Theorem of Arithmetic. #composite #numbers #prime #arithmetic #fundamental #class

Number Theory | 0:04:31

Number Theory | Lemma 1 for Fundamental Theorem of Arithmetic

Theory of numbers: 0:24:00

Theory of numbers: Fundamental theorem of arithmetic

Fundamental Theorem of 0:15:26

Fundamental Theorem of Algebra - Numberphile

Class 10 Maths|Chapter 0:14:40

Class 10 Maths|Chapter -1 Real numbers|Type IIIOn proving irrationality of numbers of the form√𝒎±√𝒏...

Prime Factorisation - 0:01:40

Prime Factorisation - The Fundamental Theorem of Arithmetic

The fundamental theorem 0:04:33

The fundamental theorem of arithmetic | Factors and multiples | Pre-Algebra | Khan Academy

The Fundamental Theorem 0:26:54

The Fundamental Theorem of Arithmetic

Class 10 Maths 0:18:17

Class 10 Maths Chapter 1 | The Fundamental Theorem of Arithmetic - Real Numbers 2022-23

Fundamental Theorem of 0:08:33

Fundamental Theorem of Arithmetic | Class 10 | Real numbers | Math's | 2020

Fundamental Theorem of 0:09:45

Fundamental Theorem of Arithmetic - Proof | Unique Prime Factorization

FUNDAMENTAL THEOREM OF 0:01:38

FUNDAMENTAL THEOREM OF ARITHMETIC | XYLEM CLASS 10 CBSE

The Fundamental Theorem 0:05:19

The Fundamental Theorem of Arithmetic | Part 1/3 | English | Class 10

Fundamental Theorem of 0:04:49

Fundamental Theorem of Arithmetic, Class - 10th

What is Fundamental 0:04:12

What is Fundamental Theorem of Arithmetic?

Fundamental Theorem of 0:11:26

Fundamental Theorem of Arithmetic

Irrationality and the 0:07:15

Irrationality and the Fundamental Theorem of Arithmetic

FUNDAMENTAL THEOREM OF 0:05:36

FUNDAMENTAL THEOREM OF ARITHMETIC

Fundamental theorem of 0:04:25

Fundamental theorem of arithmetic

Fundamental Theorem of 0:11:07

Fundamental Theorem of Algebra

Комментарии
Автор

Amazingly clear explanation! Absolutely perfect.

vethya
Автор

I know the theorem holds, but what I don't buy into this types of proofs is right in the beginning: either x is prime or it can be factorized into primes. Well, my gripe with it is that you can't use the fact that a number has a prime factorization to prove a number has a prime factorization. By that I don't mean a problem with the method of contradiction, that's fine, I mean using the result to prove the result.
The premise should be: either x is prime, or it is not. Then you work in the 'not' case, how and why it is a product of primes instead of something else.

kabzebrowski
welcome to shbcf.ru