filmov
tv
Math Olympiad | A Nice Arithmetic Sequence Progression | VIJAY Maths
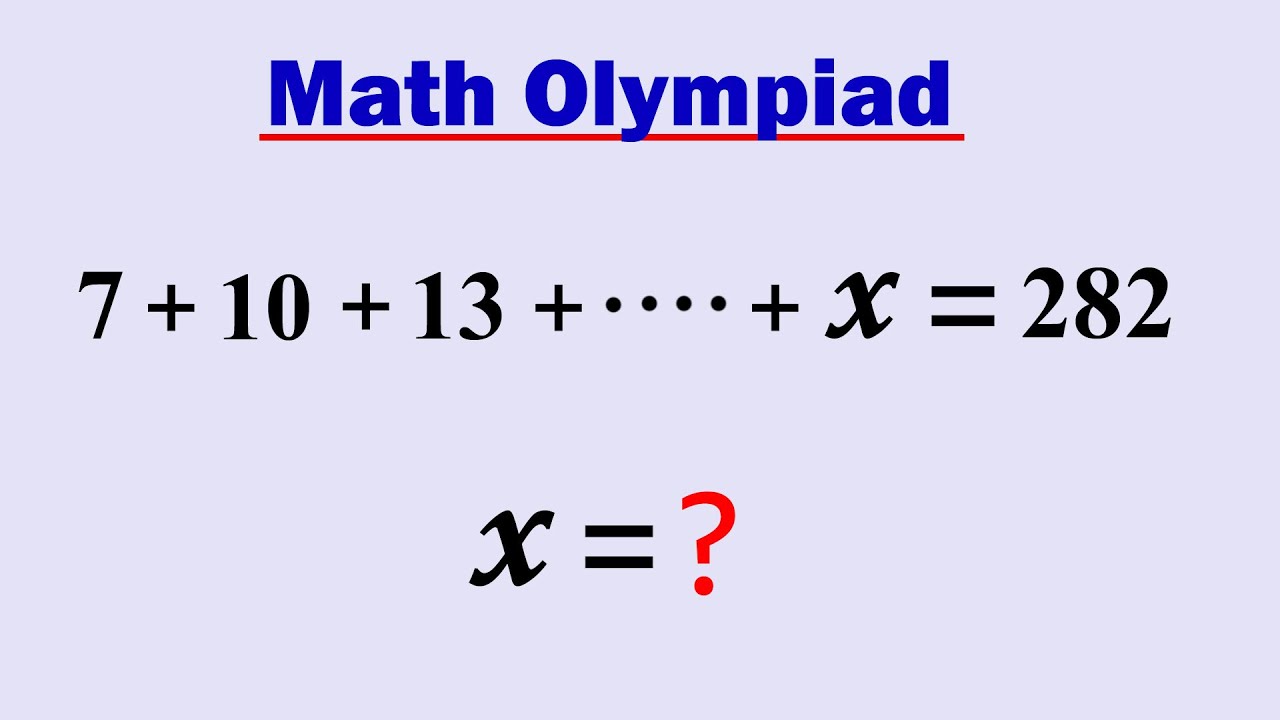
Показать описание
Also Watch our Most Viral Interesting Math Olympiad Problem:
Subscribe to our channel and press the bell icon 🔔 for daily Brainstorming Math videos →
*****************************************************************************
#matholympiad #maths #arithmetic #arithmeticsequence #arithmeticseries
Subscribe to our channel and press the bell icon 🔔 for daily Brainstorming Math videos →
*****************************************************************************
#matholympiad #maths #arithmetic #arithmeticsequence #arithmeticseries
Math Olympiad | A Very Nice Geometry Problem
Beautiful book - Combinatorics by Krishnamurthy | Math Olympiad, ISI CMI Entrance
A Nice Math Olympiad Exponential Equation 3^x = X^9
Math Olympiad | A Nice Algebra Problem | Nice square root simplification problem
A beautiful international math olympiad problem
A Math Book For Every Person In The World
You're Ready for a Maths Olympiad if you Can Solve this one...
Thailand | Math Olympiad Question | Nice Algebra Equation
Math Olympiad | A Nice Algebra Problem | Integer Solutions...
Math Olympiad | A Very Nice Geometry Problem | 2 Methods
China | Math Olympiad | A Nice Algebra Problem 👇👇👇
Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Japanese Math Olympiad Problem | A Nice Math Problem : Comparison
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
China | Math Olympiad | A Nice Algebra Problem 👇
Luxembourg - Math Olympiad Question | You should know this trick
A nice Math Olympiad Simplification Problem | Can you solve this ?
Mexico - A Nice Math Olympiad Exponential Problem
Canada | Math Olympiad | A Nice Algebra Problem
Math Olympiad | A Very Nice Algebra Problem
Japanese l Very Nice Olympiad Math Tricky Problem l How to solve for x & y ??
BOOKS FOR MATHEMATICS - GRADE 2/ OLYMPIAD BOOKS/ MOMS NEST/ V22
A Nice Algebra Math Problem. Expansion Problem. #shorts #math #algebra #olympiad #expansion #viral
Math Olympiad | A Nice Rational Equation | VIJAY Maths
Комментарии
 0:12:38
0:12:38
 0:04:39
0:04:39
 0:02:34
0:02:34
 0:06:58
0:06:58
 0:01:00
0:01:00
 0:18:41
0:18:41
 0:16:56
0:16:56
 0:01:26
0:01:26
 0:10:38
0:10:38
 0:13:46
0:13:46
 0:13:13
0:13:13
 0:13:04
0:13:04
 0:04:15
0:04:15
 0:00:52
0:00:52
 0:10:37
0:10:37
 0:02:51
0:02:51
 0:09:54
0:09:54
 0:08:36
0:08:36
 0:10:20
0:10:20
 0:08:38
0:08:38
 0:13:49
0:13:49
 0:09:45
0:09:45
 0:00:59
0:00:59
 0:07:43
0:07:43