filmov
tv
Definite integral by change of variable
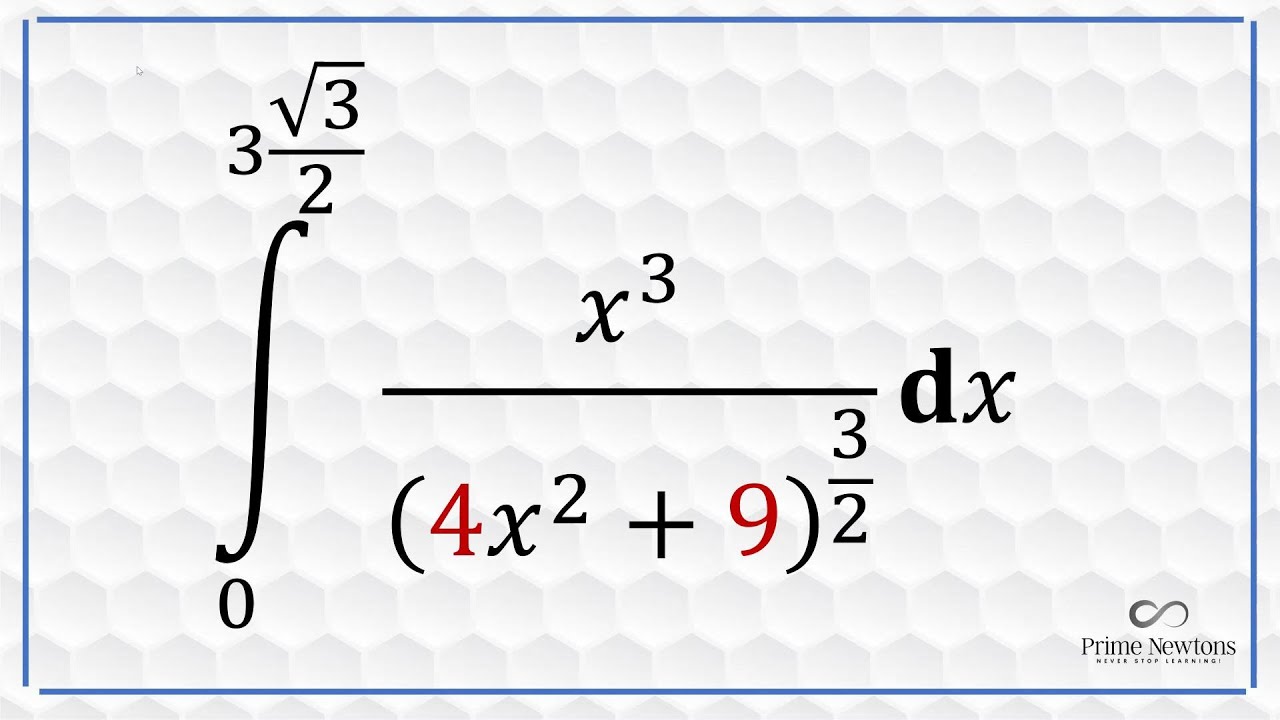
Показать описание
In this video, I showed how to use u substitution to evaluate a definite integral
Definite integral by change of variable
U-substitution With Definite Integrals
🔶43 - Evaluating Definite Integrals by U-Substitution (Change of Limits)
Definite Integral with Change of Variables, U-Substitution (Example)
Definite Integral with Change of Variables, U-Substitution (Example)
U-Substitution : When Do I Have to Change the Limits of Integration?
Definite Integral with Change of Variables, U-Substitution (Example)
Definite Integral with Change of Variables, U-Substitution (Example)
STEP 3 first half of the Hyperbolic functions booklet
definite integral by change of variables
Definite Integral with Change of Variables, U-Substitution (Example)
Definite Integral with Change of Variables, U-Substitution - Includes Natural Log (Example)
Change of Variable for Definite Integrals
Using definite integrals to find total change from a rate of change
Evaluating Definite Integrals - How to Change Bounds When Using Substitution
How to Make a Change of Variables to Evaluate a Definite Integral - Area
How to solve definite integrals (when you have to change bounds)
Definite Integral With U-Substitution
Integration by Substitution: DEFINITE INTEGRALS AND CHANGE OF LIMITS
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
evaluating definite integrals using the change of variables
Definite Integral
Integration by Substitution: Definite Integrals
How to solve Definite integral by substitution#mathematics #shorts#mathematics
Комментарии
 0:10:52
0:10:52
 0:11:03
0:11:03
 0:22:35
0:22:35
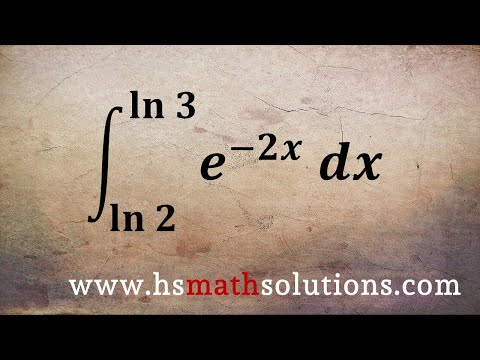 0:05:15
0:05:15
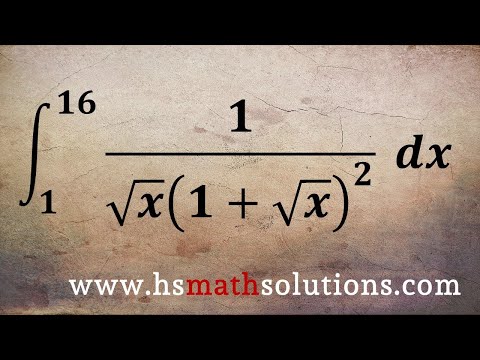 0:05:58
0:05:58
 0:08:15
0:08:15
 0:03:14
0:03:14
 0:05:52
0:05:52
 0:17:24
0:17:24
 0:13:59
0:13:59
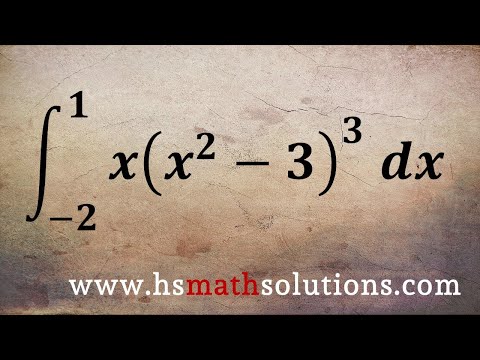 0:05:44
0:05:44
 0:05:03
0:05:03
 0:03:25
0:03:25
 0:06:18
0:06:18
 0:11:05
0:11:05
 0:08:12
0:08:12
 0:04:05
0:04:05
 0:12:56
0:12:56
 0:10:11
0:10:11
 0:00:09
0:00:09
 0:08:43
0:08:43
 0:11:05
0:11:05
 0:09:45
0:09:45
 0:01:00
0:01:00