filmov
tv
Solving A Logarithmic System

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#logarithmicequations #logarithms #algebra
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#logarithmicequations #logarithms #algebra
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Can You Solve this Logarithmic System of Equations? | Step-by-Step Tutorial
Solving a Logarithmic System
Solving A Nice Logarithmic System
Solving A Logarithmic System
Solving a System of Logarithmic Equations
Math Olympiad Question | Solving a System of Equations with Logarithm in 2 Ways
Solving a nice logarithmic system of equations
Solving system of Logarithmic Equation
517- Back-to-School Toolkit: Proven Systems for Solving Disorganization, Procrastination, and Mis...
Solving Systems of Log Equations
Natural logarithm. Solving the system of equations.
Can you solve this System of Equations Involving Logarithms & Exponents? | Quick & Simple Tu...
Solving a System of Logarithmic Equations
I Solved A System of Log Equations
Math Olympiad | Solving a System of Logarithmic Equations?
Number System : Solving Logarithms
Solving an Exponential System with Logarithms
Solving A Nice And Easy Exponential System
USA Nice Olympiad Exponential Equation: solve for a!
Solving a system of equations in logarithms with different bases. An algebra challenge.
Solving a System of Equation with Logarithms
Math Made Simple: Solving a Tricky System of Equations
Solving a System of Exponential Equations (Example)
Solve a System of Logarithmic Equations. AIME Question
Комментарии
 0:05:25
0:05:25
 0:02:46
0:02:46
 0:06:24
0:06:24
 0:08:35
0:08:35
 0:05:26
0:05:26
 0:09:50
0:09:50
 0:09:52
0:09:52
 0:05:11
0:05:11
 1:00:22
1:00:22
 0:06:00
0:06:00
 0:03:56
0:03:56
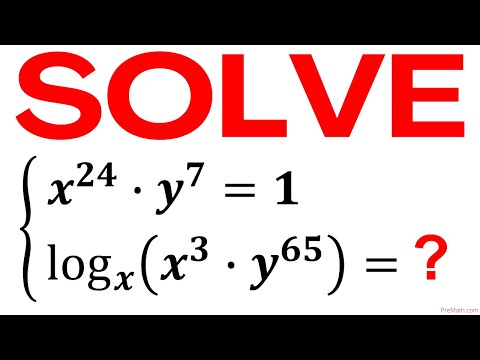 0:06:28
0:06:28
 0:00:59
0:00:59
 0:10:07
0:10:07
 0:05:57
0:05:57
 0:06:58
0:06:58
 0:10:36
0:10:36
 0:09:38
0:09:38
 0:08:05
0:08:05
 0:04:30
0:04:30
 0:06:15
0:06:15
 0:11:47
0:11:47
 0:02:20
0:02:20
 0:14:20
0:14:20