filmov
tv
Solving A Nice Logarithmic System

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts) and my first video in short form! Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Logarithms #LogarithmicEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Logarithms #LogarithmicEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving A Nice Logarithmic System
Solving a nice logarithmic system of equations
A Nice System of Logarithmic Equations
Nice Logarithmic Equation
Solving A Nice Logarithmic Equation
Solving Logarithmic Equations
A Beautiful Exponential and/or Logarithmic Equation
A Quick and Easy Logarithmic System
A Nice Exponential Equation (5^x-3^x=16)
Exponential Form to Logarithmic Form #Shorts #algebra #math #maths #mathematics #lesson #howto
solving a logarithmic equation with different bases
Can You Solve this Logarithmic System of Equations? | Step-by-Step Tutorial
A Beautiful Exponential and or Logarithmic Equation
Logarithms, Explained - Steve Kelly
A nice logarithmic equation. How to solve log2(3x+2)+1=4 - Mathsomniac
Solving A Quick and Easy Logarithmic Equation
Nice Math Olympiad Question | Learn to Solve Nice Exponential and Logarithmic Equation lnx.lny=21
Solving a System of Logarithmic Equations
How to Solve Logarithmic Equation (basics) @KasyannoEZMath
How to Solve Logarithmic Equation @KasyannoEZMath
Solving Logarithmic Exponential Equation
Solving a logarithmic equation when the bases are different. An algebraic challenge.
Logarithms... How? (NancyPi)
Solving Logarithmic Equations with Exponentials (Precalculus - College Algebra 63)
Комментарии
 0:06:24
0:06:24
 0:09:52
0:09:52
 0:10:07
0:10:07
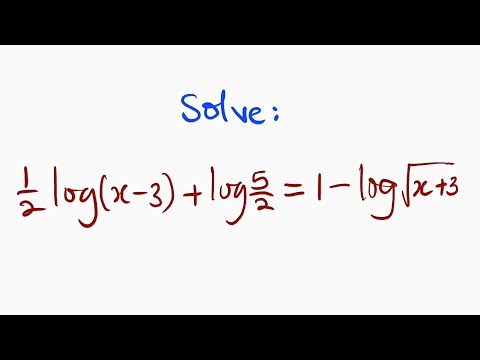 0:05:17
0:05:17
 0:09:46
0:09:46
 0:25:27
0:25:27
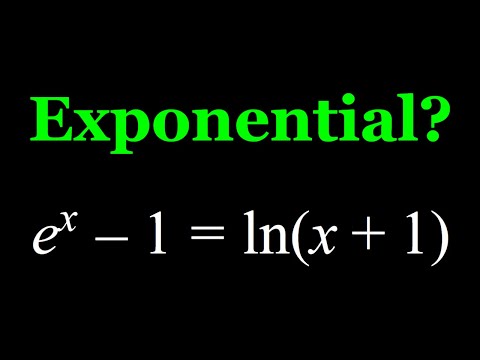 0:07:47
0:07:47
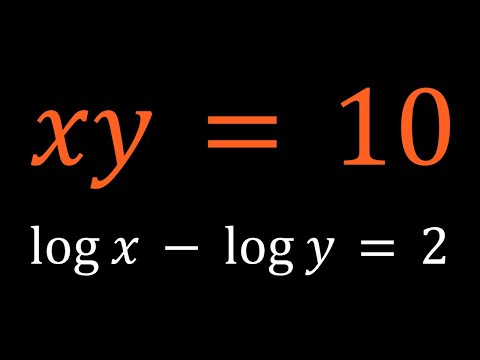 0:08:37
0:08:37
 0:06:37
0:06:37
 0:00:22
0:00:22
 0:06:02
0:06:02
 0:05:25
0:05:25
 0:07:47
0:07:47
 0:03:34
0:03:34
 0:04:22
0:04:22
 0:09:26
0:09:26
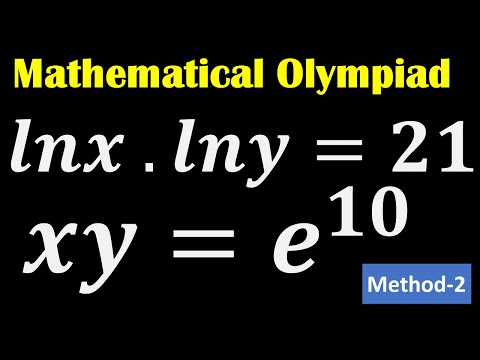 0:05:16
0:05:16
 0:05:26
0:05:26
 0:00:48
0:00:48
 0:00:58
0:00:58
 0:00:59
0:00:59
 0:05:06
0:05:06
 0:19:15
0:19:15
 1:03:43
1:03:43