filmov
tv
Mastering IGCSE Mathematics: Solving Exponential Equations | Solve for x in 5^x=1

Показать описание
Unlock the secrets of exponential equations in IGCSE Mathematics with this comprehensive tutorial. Join us as we break down the process of solving equations like 5^x=1, providing clear, step-by-step instructions and insights. Strengthen your math skills and ace your exams with this in-depth guide. Subscribe now for more IGCSE math tutorials and boost your confidence in tackling challenging problems!
#IGCSEMath
#MathTutorial
#ExponentialEquations
#MathematicsHelp
#IGCSETips
#MathematicsTutorial
#AlgebraSkills
#MathExamPrep
#LearnMath
#MathSolutions
#ExamSuccess
#MathProblems
#EducationalVideo
#StudySmart
#MathConcepts
#SchoolSuccess
#MathematicsExplained
#StudentResources
#MathHomeworkHelp
#ProblemSolvingSkills
#IGCSEMath
#MathTutorial
#ExponentialEquations
#MathematicsHelp
#IGCSETips
#MathematicsTutorial
#AlgebraSkills
#MathExamPrep
#LearnMath
#MathSolutions
#ExamSuccess
#MathProblems
#EducationalVideo
#StudySmart
#MathConcepts
#SchoolSuccess
#MathematicsExplained
#StudentResources
#MathHomeworkHelp
#ProblemSolvingSkills
Mastering IGCSE Mathematics: Solving Exponential Equations | Solve for x in 5^x=1
Mastering IGCSE Mathematics: Converting Logarithms to Exponential Form | Step-by-Step Tutorial
Exponential Equations - Algebra and Precalculus
IGCSE - Number - Exponential Growth & Decay Exercise 9.2
Solve Exponential Equations with Ease IGCSE Foundation Maths Tutorial #maths
Mastering IGCSE Mathematics: Logarithm Solving Without a Calculator | Step-by-Step Tutorial
Mastering Exponential Growth and Decay: A Comprehensive Guide for IGCSE Math
The math study tip they are NOT telling you - Math Olympian
Mastering IGCSE Mathematics: Writing Radical Fractions in Exponential Form | Exam Prep Tutorial
Ace Your IGCSE Math Exams with Exponents and Surds: A Complete Guide | Cambridge IGCSE Mathematics
Year 11 Maths IGCSE Algebra Solving Equations (TUTORIAL)
MIT Entrance Exam Problem from 1869 #Shorts #math #maths #mathematics #problem #MIT
the real reason why you're bad (or good) at math
Logarithms, Explained - Steve Kelly
Maths vs Physics
Mastering IGCSE Mathematics: Step-by-Step Guide to Evaluating Functions | f(-2) if f(x)=3-2^-x
Learn Functions – Understand In 7 Minutes
Mastering the Magic of Exponents: Unveiling the Laws of Indices for Mathematical Mastery
Mastering IGCSE Mathematics: Step-by-Step Guide to Evaluating Functions | f(3) if f(x)=3-2^-x
Mastering IGCSE Math Algebra: The Ultimate Guide to Changing the Subject of the Formula!
Solve - Exponential Equation 06 #maths #mathematics #shorts
Beyond the Classroom: Tackling Exponential Equations in Math Olympiad Training!
Mastering Exponential Growth and Decay: Quick Guide for High School Students
Exponential Growth And Decay Igcse Maths
Комментарии
 0:00:57
0:00:57
 0:02:50
0:02:50
 0:05:58
0:05:58
 0:08:55
0:08:55
 0:00:54
0:00:54
 0:02:02
0:02:02
 0:04:49
0:04:49
 0:07:42
0:07:42
 0:01:14
0:01:14
 0:00:22
0:00:22
 0:00:51
0:00:51
 0:00:48
0:00:48
 0:00:59
0:00:59
 0:03:34
0:03:34
 0:00:25
0:00:25
 0:01:20
0:01:20
 0:09:43
0:09:43
 0:03:53
0:03:53
 0:02:09
0:02:09
 0:00:46
0:00:46
 0:00:25
0:00:25
 0:08:22
0:08:22
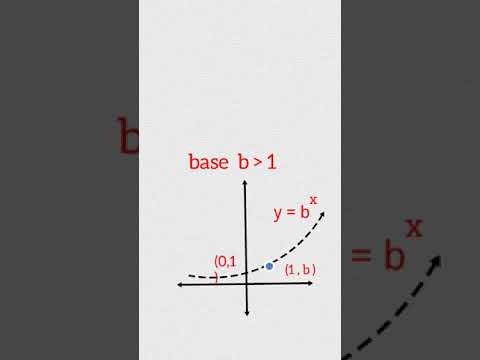 0:01:00
0:01:00
 0:30:25
0:30:25