Stationary Time Series FRM Part 1 2025 – Book 2 – Chapter 21

For FRM (Part I & Part II) video lessons, study notes, question banks, mock exams, and formula sheets covering all chapters of the FRM syllabus, click on the following link:

After completing this reading, you should be able to:

* Describe the requirements for a series to be covariance stationary.
* Define the autocovariance function and the autocorrelation function.
* Define white noise; describe independent white noise and normal (Gaussian) white noise.
* Define and describe the properties of autoregressive (AR) processes.
* Define and describe the properties of moving average (MA) processes.
* Explain how a lag operator works.
* Explain mean reversion and calculate a mean-reverting level.
* Define and describe the properties of autoregressive moving average (ARMA) processes.
* Describe the application of AR, MA, and ARMA processes.
* Describe sample autocorrelation and partial autocorrelation.
* Describe the Box-Pierce Q-statistic and the Ljung-Box Q statistic.
* Explain how forecasts are generated from ARMA models.
* Describe the role of mean reversion in long-horizon forecasts.
* Explain how seasonality is modeled in a covariance-stationary ARMA.

Welcome to our comprehensive guide to mastering quantitative analysis for the FRM Level 1 exam, focusing on five critical topics from Paper 2. In this video, we delve into Autoregressive (AR) and Moving Average (MA) models, exploring their concepts, applications, and implications in financial risk management.

Additionally, we unravel the intricacies of Autocorrelation, shedding light on its significance in analyzing time-series data and its relevance in risk assessment. We then navigate through the Partial Autocorrelation Function (PACF), providing insights into its role in understanding the relationship between sequential observations in a time series.

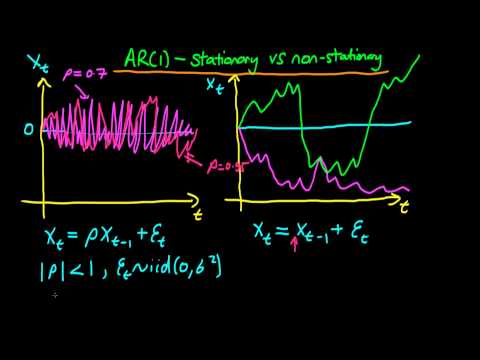
Finally, we address the crucial distinction between Stationary and Non-Stationary time series, elucidating their characteristics and the implications for risk modeling and forecasting in financial markets. Whether you're a seasoned finance professional or an aspiring risk manager, this video equips you with the knowledge and skills needed to excel in quantitative analysis for the FRM Level 1 exam. Dive in, expand your understanding, and conquer the complexities of quantitative analysis with confidence!

Don't forget to like, share, and subscribe for more insightful videos on data analysis and statistical concepts! 📊✨

#timeseriesanalysis
#timeseries
#autocorrelation
#timeseriesanalysisandforecasting
#autocorrelationfunctionintimeseries
#partialautocorrelationfunctiontimeseries
#autocorrelationfunctionanditsproperties
#timeseriesforecasting
#stationarity
#autocorrelationfunctionacftimeseries
#autocorrelationandpartialautocorrelationfunction
#timeseriesanalysisinstatistics
#quantitativeanalysis
#appliedtimeseriesanalysis
#finuture