filmov
tv
Inverse Transform Sampling - VISUALLY EXPLAINED with EXAMPLES!

Показать описание
This tutorial explains the Inverse Transform Sampling using a simple example. The proof of why the algorithm/transform works is also explained.
#sampling
#statistics
#distributions
#sampling
#statistics
#distributions
Inverse Transform Sampling - VISUALLY EXPLAINED with EXAMPLES!
Inverse Transform Sampling : Data Science Concepts
Inverse Transform Sampling | How a computer can choose random numbers from a given distribution.
Every Random Variable is a Transformation of U[0,1] (Inverse Transform Sampling)
Inverse Transform Sampling | Triangular Distribution
PDF Sampling: Inverse transform sampling (case: Plummer model)
Inverse Probability Transform & Proof (Sampling technique)
Making an animated gif for Wikipedia using Python (tutorial) - Inverse Transform Sampling
Simulating Continuous Distributions via Inverse Transform Sampling
Google Data Science interview Question | Inverse Transform Sampling | Truncated Normal | Python
Sine Curve and the Unit Circle
Lect 1 : Inverse transformation method using Rstudio
Simulating the Pareto Distribution with Inverse Transform Sampling
Random numbers: Rejection Method 01: The Idea
What is Monte Carlo simulation in statistics? Inverse transform m |Class 14,CS1-Actuarial Statistics
Accept-Reject Sampling : Data Science Concepts
Generating the Random Numbers Using the Inverse Transform Method
Monte Carlo Methods - VISUALLY EXPLAINED!
Using The Inverse CDF Method to Simulate Random Variables
AST9240 - Inversion Sampling
Rejection Sampling - VISUALLY EXPLAINED with EXAMPLES!
inverse transform technique
Code Review: Inverse transform sampling (2 Solutions!!)
Inverse CDF method
Комментарии
 0:13:29
0:13:29
 0:10:54
0:10:54
 0:02:17
0:02:17
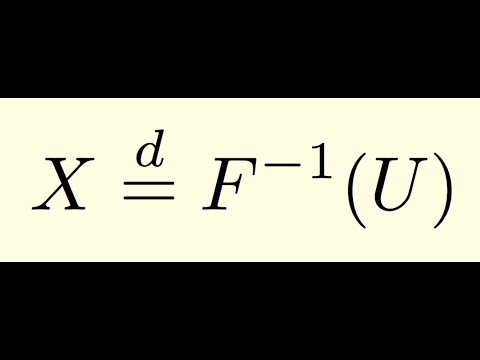 0:10:26
0:10:26
 0:07:56
0:07:56
 0:00:40
0:00:40
 0:06:43
0:06:43
 0:25:37
0:25:37
 0:18:56
0:18:56
 0:03:32
0:03:32
 0:00:27
0:00:27
 0:19:23
0:19:23
 0:09:08
0:09:08
 0:01:39
0:01:39
 0:47:51
0:47:51
 0:17:49
0:17:49
 0:46:39
0:46:39
 0:31:37
0:31:37
 0:11:40
0:11:40
 0:08:12
0:08:12
 0:15:27
0:15:27
 0:10:05
0:10:05
 0:03:35
0:03:35
 0:06:38
0:06:38