filmov
tv
f(x+1) = f(x+2) +1

Показать описание
In this video, I solved a functional equation using the f(x) =kx assumption
f(x+1) = f(x+2) +1
Solving a Functional Equation | f(x)+f(x-1)=x^2
Learn how to evaluate for a function
Functions
Finding f(0) When f(f(x))=x^2-x+1
given a function f(x), how do we evaluate f^-1(4)?
How REAL Men Integrate Functions
Design a Turing Machine for Incrementer || Decrementer || function f(x)=x+1 || f(x)=x+2 || f(x)=x-1
Given fx sketch the first and second derivative graph
Composite Functions
Learn Functions – Understand In 7 Minutes
How To Find The Inverse of a Function
The Maclaurin Series for f(x) = 1/(1-x)^2
07 - Evaluating Functions in Algebra, Part 1 (Function Notation f(x), Examples & Definition)
(fog)(x) and (gof)(x): How to find them, given f(x) and g(x).
How to Evaluate a Function f(2) Given f(x) = -x + 3
Evaluate a Function from a Graph
Dominio y rango función exponencial | f(x)=(1/2)^x | La Prof Lina M3
Find the Inverse of the Function f(x) = 1/x
5 simple unsolvable equations
How to Prove the Rational Function f(x) = 1/(x - 2) is Surjective(Onto) using the Definition
Use differentiation to find power series representation for f(x) = 1/(1+x)^2 Radius of convergence
Finding the inverse of a function
Find the values a and b that make the piecewise function continuous
Комментарии
 0:10:34
0:10:34
 0:08:59
0:08:59
 0:02:15
0:02:15
 0:06:51
0:06:51
 0:08:35
0:08:35
 0:05:58
0:05:58
 0:00:35
0:00:35
 0:07:37
0:07:37
 0:04:09
0:04:09
 0:05:23
0:05:23
 0:09:43
0:09:43
 0:11:36
0:11:36
 0:05:22
0:05:22
 0:09:53
0:09:53
 0:02:41
0:02:41
 0:00:45
0:00:45
 0:04:29
0:04:29
 0:07:23
0:07:23
 0:01:22
0:01:22
 0:00:50
0:00:50
 0:06:03
0:06:03
 0:04:11
0:04:11
 0:03:27
0:03:27
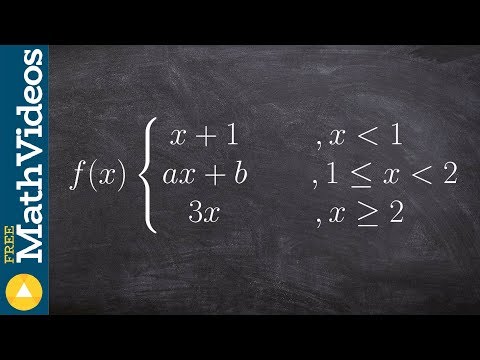 0:03:44
0:03:44