filmov
tv
Finding f(0) When f(f(x))=x^2-x+1
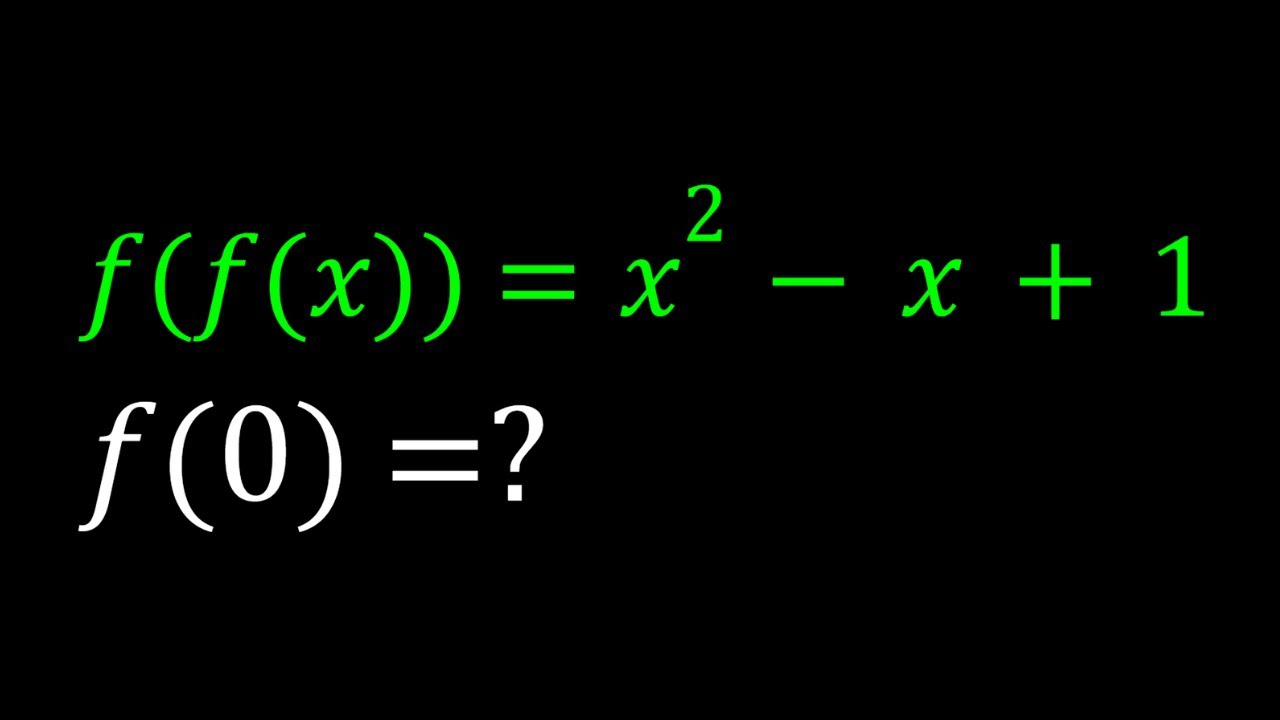
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Functions #FunctionalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #Functions #FunctionalEquations
PLAYLISTS 🎵 :
Finding f(0) When f(f(x))=x^2-x+1
Find Antiderivative f given second derivative f”(x) = 20x^3 + 12x^2 +4, f(0) = 8, f(1) = 5
If `f(x)` is continuous at `x=0`, where `f(x)=(1+2x)^(1/x)', for ' x!=0`, then `f(0)=`
Learn how to evaluate for a function
Evaluate a Function from a Graph
5 simple unsolvable equations
Let `f(x) = mx + c` and `f(0) = f'(0) = 1`. Find `f(2)`.
𝒇(𝟐𝒙−𝟑)=𝟒𝒙−𝟐, 𝒇(𝒙)=? | Olympiad Question
TMUA - Algebra and functions from Jacqueline Tyler
If `f(x)=mx+c`,`f(0)=f^`(0)=1` then `f(2)=`
If `f(x)=x^2+3x-5`, find `f(0),f(1) and `f(1/2)`.
Using the Graphs f and g to Evaluate the Expressions: f(g(3)), f(g(1)), g(f(1)), and g(f(0))
How to Compute the Difference Quotient (f(x + h) - f(x))/h
How to Evaluate Piecewise Functions with Given Values: f(-3), f(-2), f(-1), and f(0)
Find the Function Given f''(x) = 2 + cos(x), f(0) = -1, f(pi/2) = 0
Evaluate the Function f at the Values f(-2), f(-1), f(0), f(1), and f(2)
Functional equation problem - Find f(0)+f(1)+f(2) - Tip in the description.
Find x Such That f(x) = 0 [Example 1]
Given fx sketch the first and second derivative graph
If f(0)=4 and f(x+1) = 3f(x) - 2. Find f(4). Recursive function
Given a Graph, Evaluate f(0) and Solve for f(x) = -3
Composite Functions
Solving a Functional Equation | f(x)+f(x-1)=x^2
f(x) bigger than 0 | Grade 11 Functions
Комментарии
 0:08:35
0:08:35
 0:03:27
0:03:27
 0:02:43
0:02:43
 0:02:15
0:02:15
 0:04:29
0:04:29
 0:00:50
0:00:50
 0:01:14
0:01:14
 0:04:03
0:04:03
 0:17:49
0:17:49
 0:01:49
0:01:49
 0:02:19
0:02:19
 0:06:46
0:06:46
 0:03:28
0:03:28
 0:06:29
0:06:29
 0:03:57
0:03:57
 0:04:18
0:04:18
 0:00:09
0:00:09
 0:03:31
0:03:31
 0:04:09
0:04:09
 0:04:23
0:04:23
 0:05:00
0:05:00
 0:05:23
0:05:23
 0:08:59
0:08:59
 0:05:19
0:05:19