filmov
tv
Integral (sec(x))^4*tan(x) by replacing (sec(x))^2 in terms of tangent, then chain rule backwards.
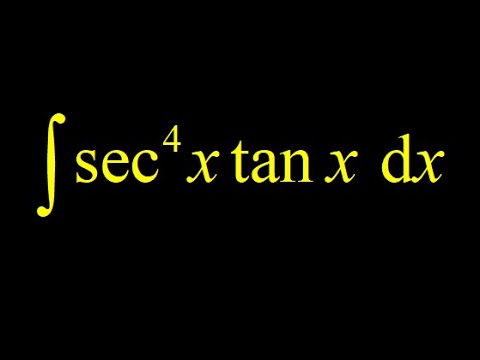
Показать описание
Questions or requests? Post your comments below, and I will respond within 24 hours.
We compute the integral (sec(x))^4*tan(x) by replacing (sec(x))^2 in terms of tangent. This leaves us with an integral with (sec(x))^2 next to powers of tan(x). This means the differential of tan(x) ((sec(x))^2dx is sitting right next to functions of tan(x), which allows us to see the chain rule backwards.
We quickly guess the antiderivative of each piece in the integrand by using the chain rule backwards, then we tack on the +C for the indefinite integral.
 0:03:27
0:03:27
 0:05:37
0:05:37
 0:04:31
0:04:31
 0:02:16
0:02:16
 0:19:45
0:19:45
 0:00:53
0:00:53
 0:07:43
0:07:43
 3:01:36
3:01:36
 0:00:43
0:00:43
 0:13:44
0:13:44
 0:18:36
0:18:36
 0:16:51
0:16:51
 0:00:37
0:00:37
 0:00:11
0:00:11
 0:12:11
0:12:11
 0:02:34
0:02:34
 0:00:12
0:00:12
 0:00:24
0:00:24
 0:07:38
0:07:38
![Integral tan(x)ln[sec(x)] l](https://i.ytimg.com/vi/lP5Jv1m2Ets/hqdefault.jpg) 0:01:55
0:01:55
 0:00:16
0:00:16
 0:12:41
0:12:41
 0:01:21
0:01:21