filmov
tv
Calculus of Variations (in Blender) // Optimization Simulations

Показать описание
Calculus of Variations (in Blender) // Optimization Simulations
Math x Blender = POWER!
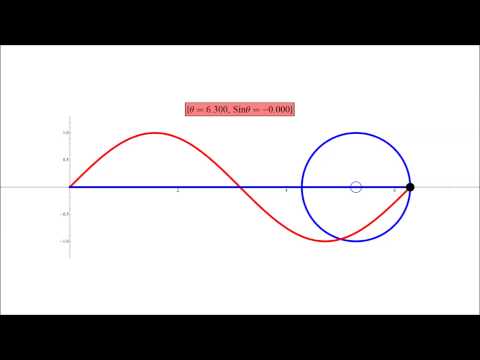
Sine Curve and the Unit Circle
Extreme Cupping Therapy! #shorts #cupping
Giving Personality to Procedural Animations using Math
[Blender 3.4] Visualizing Sine & Cosine #shorts
Physics in 10 more minutes - The principle of least action
Brachistochrone curve Fastest route for a ball 🤓
Three-Body Problem: A Precise Simulation
Allen teacher heart attack came😱😱😭 #youtubeislife #subscriber #youtubeguru #youtubecontent #shorts...
Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...
Lid-driven 3D flow Re=628
Variations of the Power 2 Mandelbulb
A sine-tangent Kaliset variation
Hexagonal Tiled Spheres
brachistochrone
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
How to Understand What Black Holes Look Like
Physics in 10 minutes - The principle of least action
Minimal surfaces and geometry of the space of cycles - Yevgeny Liokumovich
Lie group collision variational integrator - Example 3
Euler's Formula in 3D! 🌀✨️ #math #animation #mathtutoring #matheducation #mathematics
Fourier Series Spirograph Animation with Blender 3D using 2 linked arms Part 1
Комментарии
 0:10:18
0:10:18
 0:23:09
0:23:09
 0:00:27
0:00:27
 0:00:16
0:00:16
 0:15:30
0:15:30
![[Blender 3.4] Visualizing](https://i.ytimg.com/vi/uV8rkuXl9Co/hqdefault.jpg) 0:00:12
0:00:12
 0:12:02
0:12:02
 0:00:08
0:00:08
 0:01:08
0:01:08
 0:00:16
0:00:16
 0:00:15
0:00:15
 0:00:03
0:00:03
 0:00:11
0:00:11
 0:00:07
0:00:07
 0:00:21
0:00:21
 0:00:17
0:00:17
 0:00:20
0:00:20
 0:00:12
0:00:12
 0:09:19
0:09:19
 0:10:26
0:10:26
 0:12:44
0:12:44
 0:00:14
0:00:14
 0:00:27
0:00:27
 0:05:15
0:05:15