filmov
tv
Half factorial using the gamma function

Показать описание
In this video, I computed half factorial using the gamma/pi function
Half factorial using the gamma function
Half Factorial proof using the Gamma Function - (-1/2)!=sqrt(pi)
Fractional Factorials! The Gamma Function
Why is Pi here? | Half factorial without Gamma function #SoME3
The Mystery Behind This Math Miracle
Can we have 1/2 factorial?
How to Take the Factorial of Any Number
What is 1/2 factorial? - Gamma Function
Introduction to the Gamma function & the Pi function (extending the factorial!)
Extending the FACTORIAL! Gamma function derived in 60 seconds!
What Is The Factorial Of 1/2? SURPRISING (1/2)! = (√π)/2
Minus half factorial??? Yes, let's calculate this thing.
One Half Factorial ? (1/2)!
THE HALF FACTORIAL AND GAMMA FUNCTION
Can we find a value for a half factorial???
MM59: Gamma (factorial) function
The Gamma Function and (-1/2)!
What is the factorial of 1/2
1/2 Factorial, YES, Half Factorial
Proving 1! = 1 using the Gamma Function (Factorial)
The gamma function - i! Do you factorial?
How to find factorial of a decimal number? | Gamma Function | The Math Grapher
The factorial of one half?! Amazing arguments.
The Trig Hiding Inside the Factorials (And Harmonic Numbers)
Комментарии
 0:15:21
0:15:21
 0:23:36
0:23:36
 0:00:47
0:00:47
 0:13:14
0:13:14
 0:11:01
0:11:01
 0:10:53
0:10:53
 0:26:31
0:26:31
 0:19:01
0:19:01
 0:18:01
0:18:01
 0:00:56
0:00:56
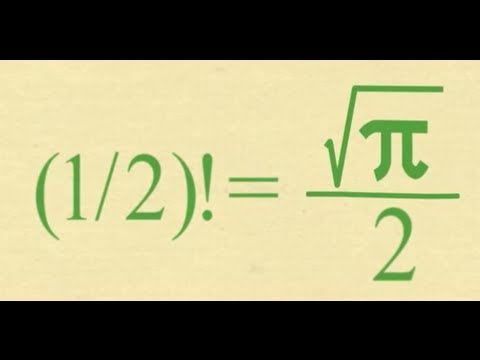 0:04:55
0:04:55
 0:05:52
0:05:52
 0:04:21
0:04:21
 0:09:34
0:09:34
 0:05:26
0:05:26
 0:12:03
0:12:03
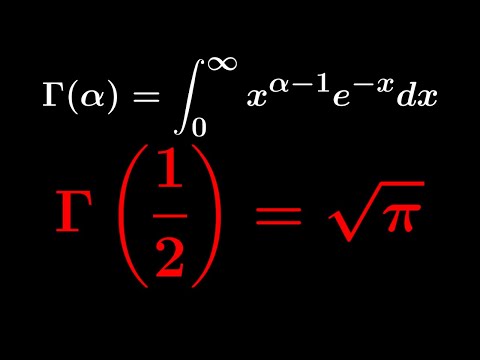 0:09:16
0:09:16
 0:02:14
0:02:14
 0:01:59
0:01:59
 0:05:44
0:05:44
 0:11:01
0:11:01
 0:04:35
0:04:35
 0:04:48
0:04:48
 0:19:06
0:19:06