filmov
tv
Graphing Functions and Their Derivatives
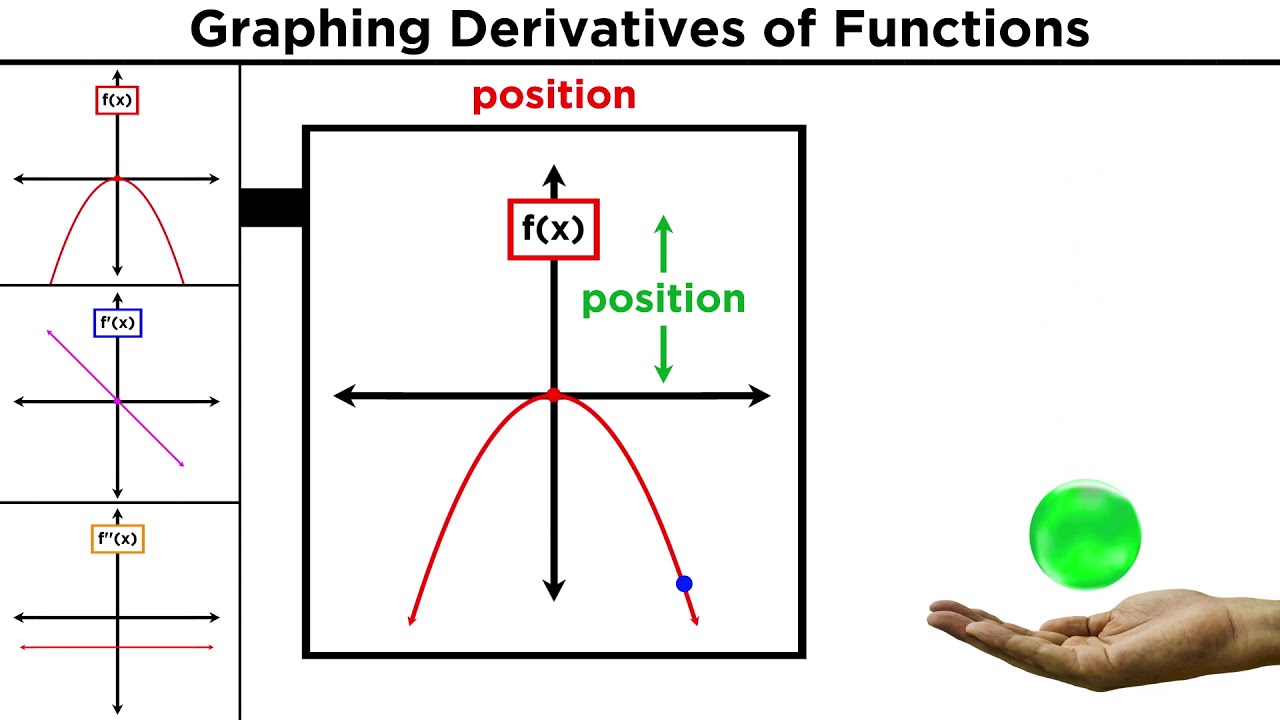
Показать описание
We know how to graph functions, and we know how to take derivatives, so let's graph some derivatives! Many students find that this hurts their brain, but it's just about practice! Remember that the value of a function and the rate of change of that function at a particular point are completely unrelated! A function may be positive but have a negative rate of change, or vice versa. Let's learn how to graph derivatives intuitively, and then some applications of this in physics!
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Graphing Functions and Their Derivatives
Given fx sketch the first and second derivative graph
Calculus AB/BC – 5.8 Sketching Graphs of Functions and Their Derivatives
Sketching a Derivative from the Graph of a Function
Connecting f, f', and f'' graphically | AP Calculus AB | Khan Academy
Graphs of functions and their derivatives example 1 | Differential Calculus | Khan Academy
Matching Graphs of Functions and Their Derivatives
Identifying the graphs of a function and its derivatives
CALCULATING, 'areas using integrals is a central application of calculus.'
Sketching Functions From The Graphs of Derivatives
Finding derivatives from a graph
Curve Sketching - Graphing Functions Using Derivatives | Calculus
The graphical relationship between a function & its derivative (part 1) | Khan Academy
Determining Derivatives from Graphs (1 of 3: Identifying major features)
Graphing using derivatives | Derivative applications | Differential Calculus | Khan Academy
AP Calculus AB - 5.8 Sketching Graphs of Functions and Their Derivatives
📈Graphing📉 functions and their derivatives 🤯🤯 #apcalculus #apcalc #unit5 #shorts
Graphing Derivatives - Made Easy
sketching the graph of derivatives (6 examples)
Determining Derivatives from Graphs (2 of 3: Considering sign of the gradient)
Visually determining antiderivative | AP Calculus AB | Khan Academy
Graphing a Basic Function
Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
Graphs from Derivatives, Part 1
Комментарии
 0:13:06
0:13:06
 0:04:09
0:04:09
 0:11:42
0:11:42
 0:08:44
0:08:44
 0:05:36
0:05:36
 0:05:57
0:05:57
 0:02:46
0:02:46
 0:10:56
0:10:56
 0:00:51
0:00:51
 0:06:17
0:06:17
 0:05:21
0:05:21
 0:22:02
0:22:02
 0:05:05
0:05:05
 0:07:15
0:07:15
 0:20:31
0:20:31
 0:23:04
0:23:04
 0:00:54
0:00:54
 0:04:21
0:04:21
 0:17:33
0:17:33
 0:07:22
0:07:22
 0:04:27
0:04:27
 0:05:36
0:05:36
 0:07:16
0:07:16
 0:08:00
0:08:00