filmov
tv
Calculate the Last 2 Digits of a Tower of Powers in Number Theory

Показать описание
This is a tutorial on Number Theory and how to Find the last 2 digits of 7^(7^7)
Best place to start is with the (7^7) .
Use Eulers Totient Function to find 7^7 is congruent to alpha mod phi(100) = 40 , then phi(40)=16.
phi(100) = phi(25)*phi(4) which is in the form of phi(p^a)=p^(a-1)(p-1)
We use this technique again for phi(40)= phi(8)*phi(5) =16
We then are left with 7^7 mod 16 which is 7.
The final part is to find 7^7 mod 100 which is 43.
#algebra
#euclidsalgorithm
#euclid_division_algorithm
#euclidsdivisionlemma
#euclidean
#mathtricks
#numbersystem
#numbers
#numbertheory
#bernoulli
Best place to start is with the (7^7) .
Use Eulers Totient Function to find 7^7 is congruent to alpha mod phi(100) = 40 , then phi(40)=16.
phi(100) = phi(25)*phi(4) which is in the form of phi(p^a)=p^(a-1)(p-1)
We use this technique again for phi(40)= phi(8)*phi(5) =16
We then are left with 7^7 mod 16 which is 7.
The final part is to find 7^7 mod 100 which is 43.
#algebra
#euclidsalgorithm
#euclid_division_algorithm
#euclidsdivisionlemma
#euclidean
#mathtricks
#numbersystem
#numbers
#numbertheory
#bernoulli
How To Calculate Faster than a Calculator
How to Calculate Faster than a Calculator - Mental Math #1
How to Calculate Faster than a Calculator - Mental Maths #1
CALCULATE Last 2 digits and last 3 digits of an expression | NUMBER SYSTEM PART 12
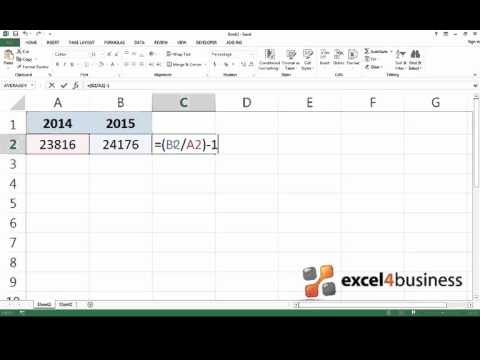
How to Calculate Percent Change in Excel
Calculate the any power of any number using Scientific Calculator
How to Calculate Faster than a Calculator - Mental Maths #2| Addition and Subtraction
Trick 🔥 for table of 80
How I learned to Calculate Extremely Fast
Calculate Percentage easy way #%#percentage #calculus#calculator #mobilecalcutorhacks
How to calculate the power of a number | Basics of Mathematics
How to calculate percentage on scientific calculator #scintific #calculator
How to Calculate Faster than a Calculator. Mental Maths-6 (50k Subscribers special)
Saying 'I Love You' in Maths Equation
How to Calculate the Odds of Winning the Lottery
Excel Formula to Calculate Percentage change #excelshorts
Trick to calculate salary increment 💪😎 #advancedexcel #excelshorts
Salary was 35000 which increased by 15%. Calculate new salary. Topic #percentage #math #percent
How to calculate a grade / percentage #calculategrade #division #teacher #fyp #education
How to calculate Negative Indices Fractions? #math #tutor #fraction #indices #power #exponents #x^-2
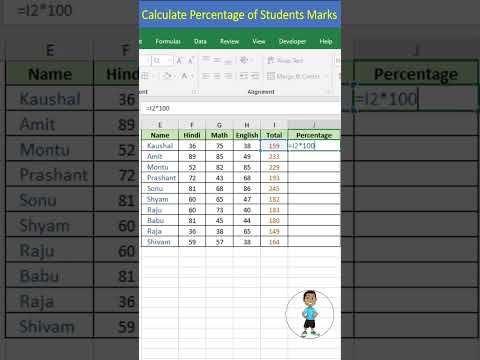
Calculate Percentage of Students Marks in Excel #excel #exceltips #exceltutorial #msexcel #shorts
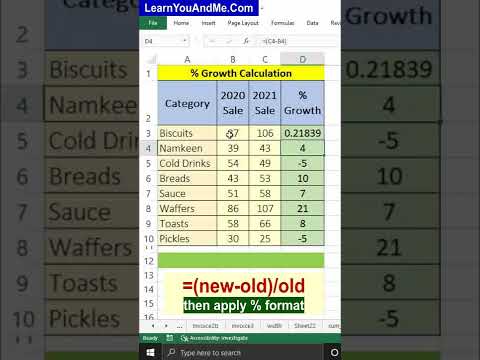
Calculate % increase or percent growth in Excel | Sale Growth percent in Excel | Percent increase
Calculate the number of Years between two Dates in Excel
How to Calculate Percent Difference Between Two Numbers in Excel
Комментарии
 0:00:30
0:00:30
 0:07:20
0:07:20
 0:05:42
0:05:42
 0:21:16
0:21:16
 0:00:56
0:00:56
 0:00:21
0:00:21
 0:08:00
0:08:00
 0:00:07
0:00:07
 0:05:18
0:05:18
 0:00:54
0:00:54
 0:02:42
0:02:42
 0:00:15
0:00:15
 0:10:29
0:10:29
 0:00:50
0:00:50
 0:08:18
0:08:18
 0:00:26
0:00:26
 0:00:30
0:00:30
 0:00:23
0:00:23
 0:00:55
0:00:55
 0:00:36
0:00:36
 0:00:22
0:00:22
 0:01:00
0:01:00
 0:00:31
0:00:31
 0:01:19
0:01:19