1996 IMO Problem #4

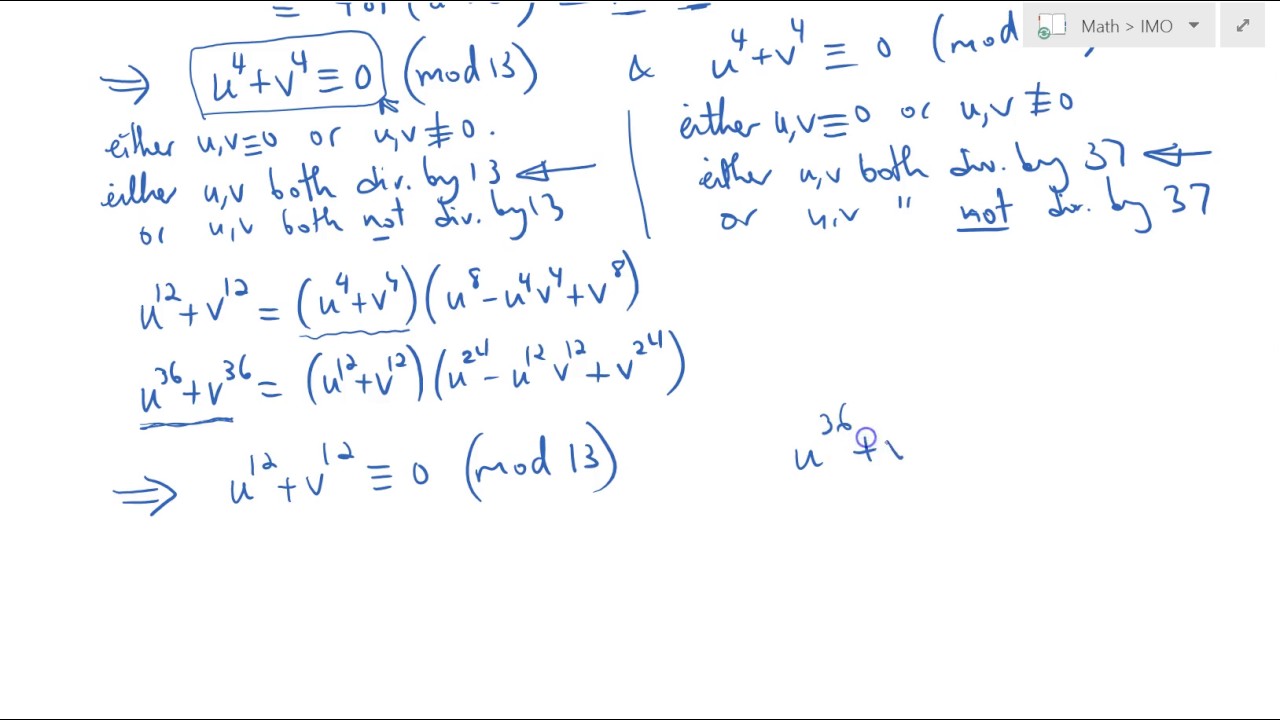
preview_player
Показать описание

  1. Mr. Math
  2. 1996 IMO
Рекомендации по теме
1996 IMO Problem 0:11:16

1996 IMO Problem #4

British Mathematical Olympiad| 0:10:16

British Mathematical Olympiad| Round 2 : 1996 Problem 4| IMO| NAT| GAT| GRE| GMAT| IIT JEE Prep|

1995 IMO Problem 0:16:15

1995 IMO Problem #4

1996 IMO Problem 0:12:01

1996 IMO Problem #5

1997 IMO Problem 0:18:43

1997 IMO Problem #4

Solve an IMO 0:04:56

Solve an IMO problem in 5 minutes (1975 Problem 4)

1994 IMO Problem 0:13:04

1994 IMO Problem #4

1996 IMO Problem 0:21:24

1996 IMO Problem #3

1996 IMO Problem 0:18:17

1996 IMO Problem #1

[Very first IMO 0:09:37

[Very first IMO in history] 1959 IMO Problem #4: Triangle and Geometric Mean

2020 IMO Problem 0:03:55

2020 IMO Problem 1 Solution: Weird Geometry with angle ratios

1996 IMO Problem 0:19:24

1996 IMO Problem #2

The Legend of 0:08:45

The Legend of Question Six - Numberphile

1992 IMO Problem 0:09:41

1992 IMO Problem #4

Geometry Problem in 0:07:07

Geometry Problem in IMO (1968) Q1

1991 IMO Problem 0:10:12

1991 IMO Problem #4

1996 IMO Problem 0:12:41

1996 IMO Problem #2 (Projective Geometry)

2015 IMO PROBLEM 0:10:55

2015 IMO PROBLEM 4 SOLUTION

2014 IMO Problem 0:14:49

2014 IMO Problem #4

1962 IMO Problem 0:15:51

1962 IMO Problem #4

1989 IMO Problem 0:13:45

1989 IMO Problem #4

1985 IMO Problem 0:13:55

1985 IMO Problem #4

1999 IMO Problem 0:13:00

1999 IMO Problem #6

1964 IMO Problem 0:08:06

1964 IMO Problem #4

Комментарии
Автор

The much easier way would be just solve for a and b and get 481b=16x^2-15y^2 and 481a = 15x^2+16y^2 and therefore 481|16x^2-15y^2 and 481|15x^2+16y^2. Some simple modular arithmetic we can conclude 481|x^2 and 481|y^2.

cr
Автор

Hey Mr. Nal! Love your lectures, they are quite helpful and fun! Could you please do some modern olympiad problems? (ISL, etc.) Thank you!

realquarterb
Автор

Your videos are great... Good problems and nice solutions... Thanks a lot

khaledqaraman
Автор

How does one think of considering u^4 + v^4? It seems very arbitrary to come up with. In the process of problem solving, how does one get to the ‘crux’ as you called it?

JohnSmith-vqho
Автор

Just when I thought I was good at Maths

eroskuikel
Автор

When I was in 8th grade my teacher gave me this problem, I found that Min is 481^2 but I didn't proof it:]
I didn't know that it is IMO problem

mardymsyz