filmov
tv
How to solve Quadratic Equations by Completing the Square
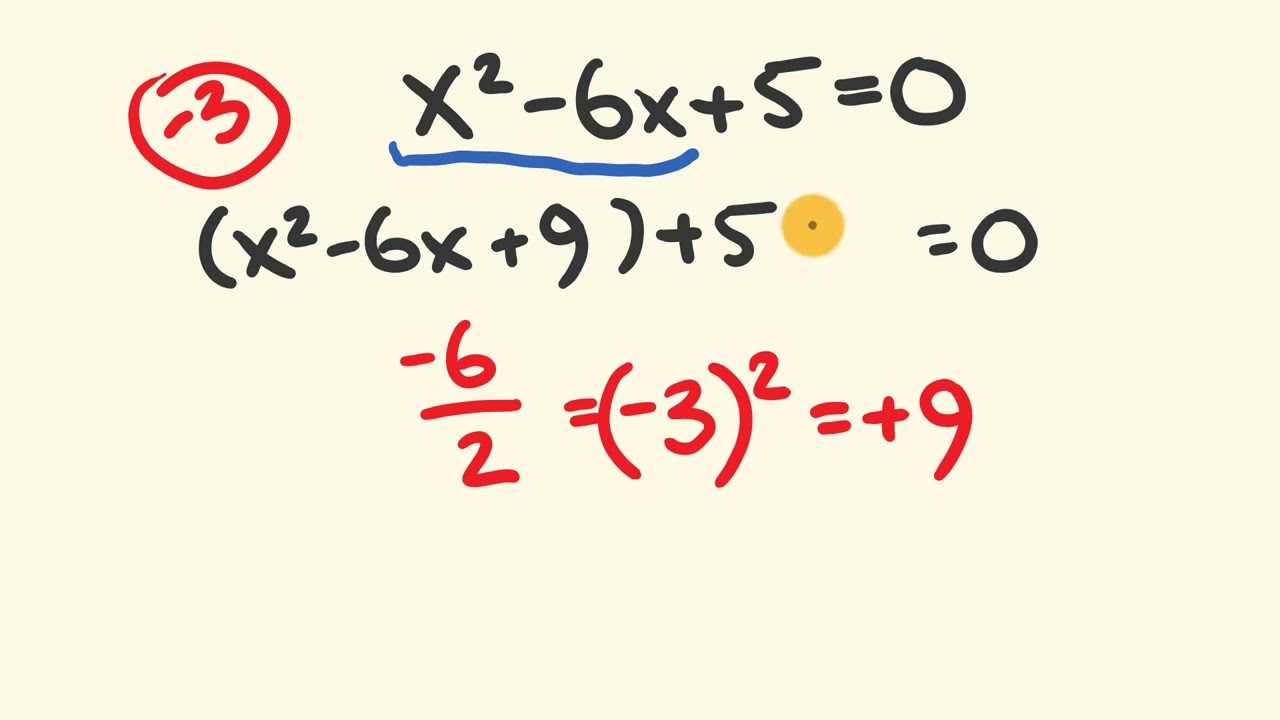
Показать описание
In this video we look at how to use completing the square to solve quadratic equations using an easy example.
It really helps and is appreciated!
It really helps and is appreciated!
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
How To Solve Quadratic Equations Using The Quadratic Formula
Quadratic Equations | Solve by factoring | Free Math Videos
Solve quadratic equation by factorisation
Solve Quadratic Equations By Factoring - Simple Trick No Fuss!
How to Solve Quadratic Equations using the Quadratic Formula
How to Solve Quadratic Equations by Factoring (NancyPi)
Solving Quadratic Equations (5 Methods)
How to Solve Quadratic Equations in 1 Minute!
Solving a quadratic equation by factoring | Algebra II | Khan Academy
Solving Quadratic Equations by Factoring│Algebra
GCSE Maths - Solving Quadratics Using the Quadratic Formula #51
4 WAYS TO SOLVE A QUADRATIC EQUATION | Algebra 1 & 2 | Factoring, Square Roots, Quadratic Formul...
Solving Quadratic Equations by Factoring - Basic Examples
How to Solve Quadratic Equations using Three Methods - When Leading Coefficient is Not One
Learn how to solve a quadratic equation by factoring
Solving Quadratic Equations By Completing The Square
How to Solve Quadratic Equations - Using 3 Different Methods
Quadratic Equations Grade 10
01 - Solving Equations in Quadratic Form - Part 1 (Learn to Solve Equations in Algebra)
How To Solve Quadratic Equations By Completing The Square
QUADRATIC EQUATIONS | Solution by Factorization.
The Maths Prof: Solve Quadratic Equations using Quadratic Formula
Solving Quadratic Equations using Quadratic Formula - Quadratic Equations
Комментарии
 0:12:29
0:12:29
 0:05:56
0:05:56
 0:02:43
0:02:43
 0:09:05
0:09:05
 0:06:31
0:06:31
 0:10:16
0:10:16
 0:11:11
0:11:11
 0:08:43
0:08:43
 0:13:35
0:13:35
 0:06:22
0:06:22
 0:22:30
0:22:30
 0:05:27
0:05:27
 0:08:20
0:08:20
 0:07:19
0:07:19
 0:15:43
0:15:43
 0:02:40
0:02:40
 0:07:57
0:07:57
 0:09:30
0:09:30
 0:05:17
0:05:17
 0:37:08
0:37:08
 0:13:07
0:13:07
 0:14:18
0:14:18
 0:07:18
0:07:18
 0:09:06
0:09:06