filmov
tv
monotonic and bounded sequence always convergent Real Analysis IIT Jam 2016 Mathematics solution

Показать описание
For Notes and Practice set WhatsApp @ 8130648819 or visit our Website
Join this channel to get access to perks:
The algebraic and order properties of R, suprema and infima, the completeness property of R, the Archimedean property, density of rational numbers in R, characterization of intervals, neighborhoods, open sets, closed sets, limit points of a set, isolated points, closure, complements, idea of uncountability of R.
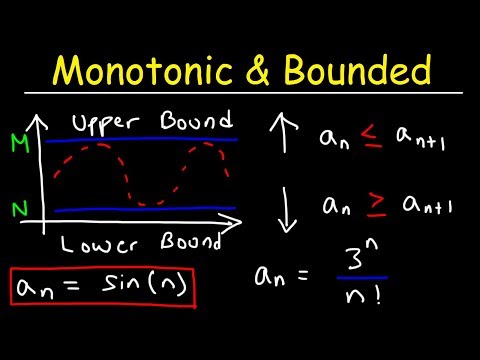
Sequences, bounded sequence, limit of a sequence, convergent sequences, limit theorems, monotone sequences, monotone convergence theorem, subsequences, convergence and divergence criteria, existence of monotonic subsequences (idea only), Bolzano-Weierstrass theorem for sequences and sets, definition of Cauchy sequence, Cauchy's convergence criterion, limit superior and limit inferior of a sequence.
Definition of infinite series, sequence of partial sums, convergence of infinite series, Cauchy criterion, absolute and conditional convergence, convergence via boundedness of sequence of partial sums, tests of convergence: comparison test, limit comparison test, ratio test, Cauchy's nth root test alternating series, Leibniz test.
Functions of One Real Variable: Limit, continuity, intermediate value property, differentiation, Rolle’s Theorem, mean value theorem, L'Hospital rule, Taylor's theorem, maxima, and minima.
Functions of Two or Three Real Variables: Limit, continuity, partial derivatives, differentiability, maxima, and minima.
Integral Calculus: Integration as the inverse process of differentiation, definite integrals, and their properties, fundamental theorem of calculus. Double and triple integrals, change of order of integration, calculating surface areas and volumes using double integrals, calculating volumes using triple integrals.
Differential Equations: Ordinary differential equations of the first order of the form y'=f(x,y), Bernoulli’s equation, exact differential equations, integrating factor, orthogonal trajectories, homogeneous differential equations, variable separable equations, linear differential equations of second order with constant coefficients, Method of variation of parameters, Cauchy-Euler equation.
Vector Calculus: Scalar and vector fields, gradient, divergence, curl, line integrals, surface integrals, Green, Stokes, and Gauss theorems.
Group Theory: Groups, subgroups, Abelian groups, non-Abelian groups, cyclic groups, permutation groups, normal subgroups, Lagrange's Theorem for finite groups, group homomorphism, and basic concepts of quotient groups.
Linear Algebra: Finite dimensional vector spaces, linear independence of vectors, basis, dimension, linear transformations, matrix representation, range space, null space, rank-nullity theorem. Rank and inverse of a matrix, determinant, solutions of systems of linear equations, consistency conditions, eigenvalues, and eigenvectors for matrices, Cayley-Hamilton theorem.
Real Analysis: Interior points, limit points, open sets, closed sets, bounded sets, connected sets, compact sets, completeness of R. Power series (of real variable), Taylor’s series, radius and interval of convergence, term-wise differentiation, and integration of power series.
IIT JAM Syllabus 2021 for Mathematical Statistics (MS)
The JAM test paper for Mathematical Statistics consists of two subjects which are Mathematics and Statistics. The weightage given to Mathematics is 40 percent and Statistics is 60 percent. Aspirants can go through the detailed IIT JAM Mathematical Statistics syllabus here. Find out the important topics for the Mathematical Statistics course below:
IIT JAM 2022 Mathematics Syllabus
Sequences and Series: Convergence of sequences of real numbers, Comparison, root and ratio tests for convergence of series of real numbers.
Differential Calculus: Limits, continuity, and differentiability of functions of one and two variables. Rolle's theorem, mean value theorems, Taylor's theorem, indeterminate forms, maxima and minima of functions of one and two variables.
Integral Calculus: Fundamental theorems of integral calculus. Double and triple integrals, applications of definite integrals, arc lengths, areas, and volumes.
Matrices: Rank, inverse of a matrix, Systems of linear equations, Linear transformations, eigenvalues, and eigenvectors. Cayley-Hamilton theorem, symmetric, skew-symmetric, and orthogonal matrices.
monotonic and bounded sequence always convergent Real Analysis IIT Jam 2016 Mathematics solution
En Jam MA 2016, 31
Key (a, c)
Join this channel to get access to perks:
The algebraic and order properties of R, suprema and infima, the completeness property of R, the Archimedean property, density of rational numbers in R, characterization of intervals, neighborhoods, open sets, closed sets, limit points of a set, isolated points, closure, complements, idea of uncountability of R.
Sequences, bounded sequence, limit of a sequence, convergent sequences, limit theorems, monotone sequences, monotone convergence theorem, subsequences, convergence and divergence criteria, existence of monotonic subsequences (idea only), Bolzano-Weierstrass theorem for sequences and sets, definition of Cauchy sequence, Cauchy's convergence criterion, limit superior and limit inferior of a sequence.
Definition of infinite series, sequence of partial sums, convergence of infinite series, Cauchy criterion, absolute and conditional convergence, convergence via boundedness of sequence of partial sums, tests of convergence: comparison test, limit comparison test, ratio test, Cauchy's nth root test alternating series, Leibniz test.
Functions of One Real Variable: Limit, continuity, intermediate value property, differentiation, Rolle’s Theorem, mean value theorem, L'Hospital rule, Taylor's theorem, maxima, and minima.
Functions of Two or Three Real Variables: Limit, continuity, partial derivatives, differentiability, maxima, and minima.
Integral Calculus: Integration as the inverse process of differentiation, definite integrals, and their properties, fundamental theorem of calculus. Double and triple integrals, change of order of integration, calculating surface areas and volumes using double integrals, calculating volumes using triple integrals.
Differential Equations: Ordinary differential equations of the first order of the form y'=f(x,y), Bernoulli’s equation, exact differential equations, integrating factor, orthogonal trajectories, homogeneous differential equations, variable separable equations, linear differential equations of second order with constant coefficients, Method of variation of parameters, Cauchy-Euler equation.
Vector Calculus: Scalar and vector fields, gradient, divergence, curl, line integrals, surface integrals, Green, Stokes, and Gauss theorems.
Group Theory: Groups, subgroups, Abelian groups, non-Abelian groups, cyclic groups, permutation groups, normal subgroups, Lagrange's Theorem for finite groups, group homomorphism, and basic concepts of quotient groups.
Linear Algebra: Finite dimensional vector spaces, linear independence of vectors, basis, dimension, linear transformations, matrix representation, range space, null space, rank-nullity theorem. Rank and inverse of a matrix, determinant, solutions of systems of linear equations, consistency conditions, eigenvalues, and eigenvectors for matrices, Cayley-Hamilton theorem.
Real Analysis: Interior points, limit points, open sets, closed sets, bounded sets, connected sets, compact sets, completeness of R. Power series (of real variable), Taylor’s series, radius and interval of convergence, term-wise differentiation, and integration of power series.
IIT JAM Syllabus 2021 for Mathematical Statistics (MS)
The JAM test paper for Mathematical Statistics consists of two subjects which are Mathematics and Statistics. The weightage given to Mathematics is 40 percent and Statistics is 60 percent. Aspirants can go through the detailed IIT JAM Mathematical Statistics syllabus here. Find out the important topics for the Mathematical Statistics course below:
IIT JAM 2022 Mathematics Syllabus
Sequences and Series: Convergence of sequences of real numbers, Comparison, root and ratio tests for convergence of series of real numbers.
Differential Calculus: Limits, continuity, and differentiability of functions of one and two variables. Rolle's theorem, mean value theorems, Taylor's theorem, indeterminate forms, maxima and minima of functions of one and two variables.
Integral Calculus: Fundamental theorems of integral calculus. Double and triple integrals, applications of definite integrals, arc lengths, areas, and volumes.
Matrices: Rank, inverse of a matrix, Systems of linear equations, Linear transformations, eigenvalues, and eigenvectors. Cayley-Hamilton theorem, symmetric, skew-symmetric, and orthogonal matrices.
monotonic and bounded sequence always convergent Real Analysis IIT Jam 2016 Mathematics solution
En Jam MA 2016, 31
Key (a, c)
Комментарии
 0:31:23
0:31:23
 0:03:42
0:03:42
 0:09:04
0:09:04
 0:08:02
0:08:02
 0:41:57
0:41:57
 0:06:31
0:06:31
 0:10:49
0:10:49
 0:13:44
0:13:44
 0:43:22
0:43:22
 0:04:46
0:04:46
 0:11:54
0:11:54
 0:11:51
0:11:51
 0:05:47
0:05:47
 0:32:53
0:32:53
 0:27:28
0:27:28
 0:08:56
0:08:56
 0:08:20
0:08:20
 0:12:18
0:12:18
 0:13:14
0:13:14
 0:13:02
0:13:02
 0:11:34
0:11:34
 0:03:41
0:03:41
 0:17:31
0:17:31
 0:06:26
0:06:26