filmov
tv
Intuition of Euler's Formula WITHOUT Taylor Series
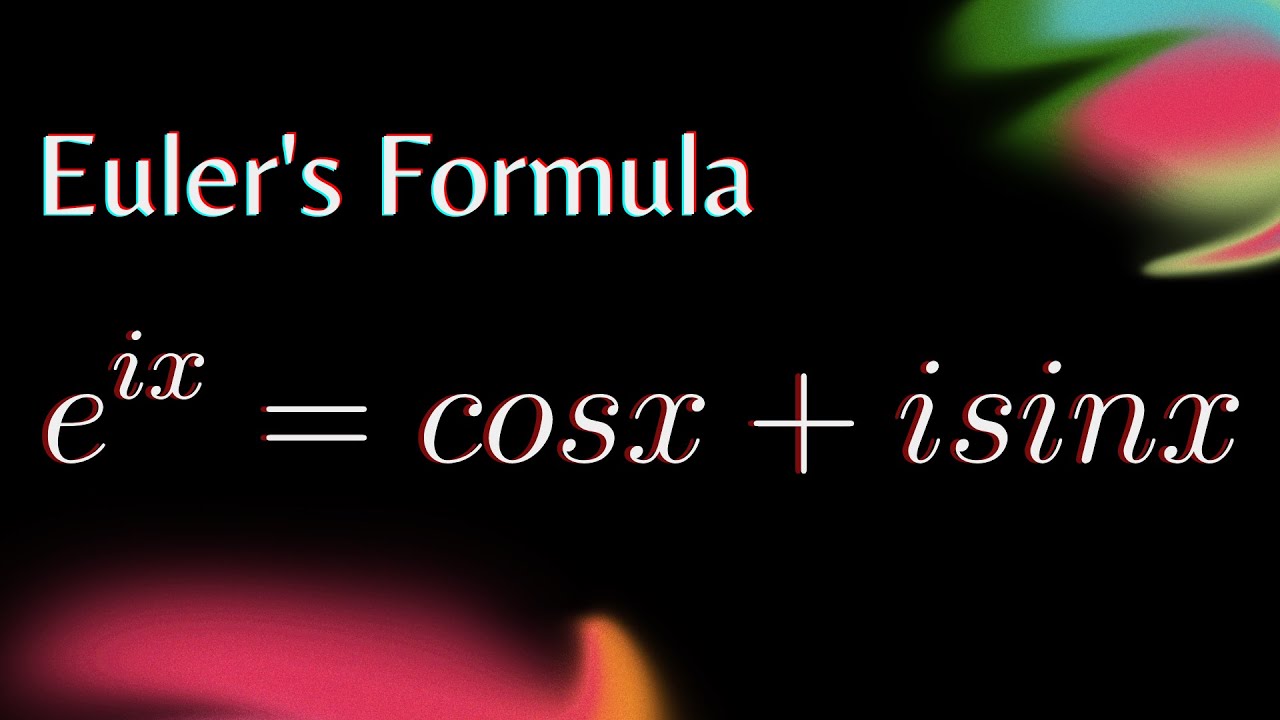
Показать описание
Here we discuss how to come across Euler's formula without needing to use Taylor expansion, instead exploring the dynamics of a particle undergoing circular motion. Enjoy :3
Intuition of Euler's Formula WITHOUT Taylor Series
e^(iπ) in 3.14 minutes, using dynamics | DE5
Proof of Euler's Formula Without Taylor Series
Visualizing Euler's formula.
Understanding Euler's Formula | BetterExplained
e to the (i pi): the Most Intuitive Explanation // #SoME2 on Euler's Formula π
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
What's so special about Euler's number e? | Chapter 5, Essence of calculus
Euler's formula with introductory group theory
The most beautiful equation in math, explained visually [Euler’s Formula]
Grant Sanderson (3Blue1Brown): Best Way to Learn Math | AI Podcast Clips
Euler's Formula and Sine Wave
Euler-Lagrange equation explained intuitively - Lagrangian Mechanics
Necessity of complex numbers
Informal Proof of Euler's Formula (1 of 2: Exponential calculus)
Euler's method | Differential equations| AP Calculus BC | Khan Academy
Euler's Totient Theorem and Fermat's Little Theorem - Complete Proof & Intuition
Why do trig functions appear in Euler's formula?
What is Euler's formula actually saying? | Ep. 4 Lockdown live math
Imaginary Numbers Are Real [Part 1: Introduction]
Euler's Equation
Euler’s identity proof for calculus 2 students!
Laplacian intuition
Sine Curve and the Unit Circle
Комментарии
 0:48:24
0:48:24
 0:04:08
0:04:08
 0:03:57
0:03:57
 0:00:12
0:00:12
 0:09:54
0:09:54
 0:09:43
0:09:43
 0:00:38
0:00:38
 0:13:50
0:13:50
 0:24:28
0:24:28
 0:26:57
0:26:57
 0:03:22
0:03:22
 0:02:12
0:02:12
 0:18:22
0:18:22
 0:07:39
0:07:39
 0:15:21
0:15:21
 0:10:07
0:10:07
 0:15:29
0:15:29
 0:13:11
0:13:11
 0:51:16
0:51:16
 0:05:47
0:05:47
 0:00:16
0:00:16
 0:07:19
0:07:19
 0:05:31
0:05:31
 0:00:27
0:00:27