filmov
tv
MATH1131 Linear Algebra: Chapter 4 Problem 17
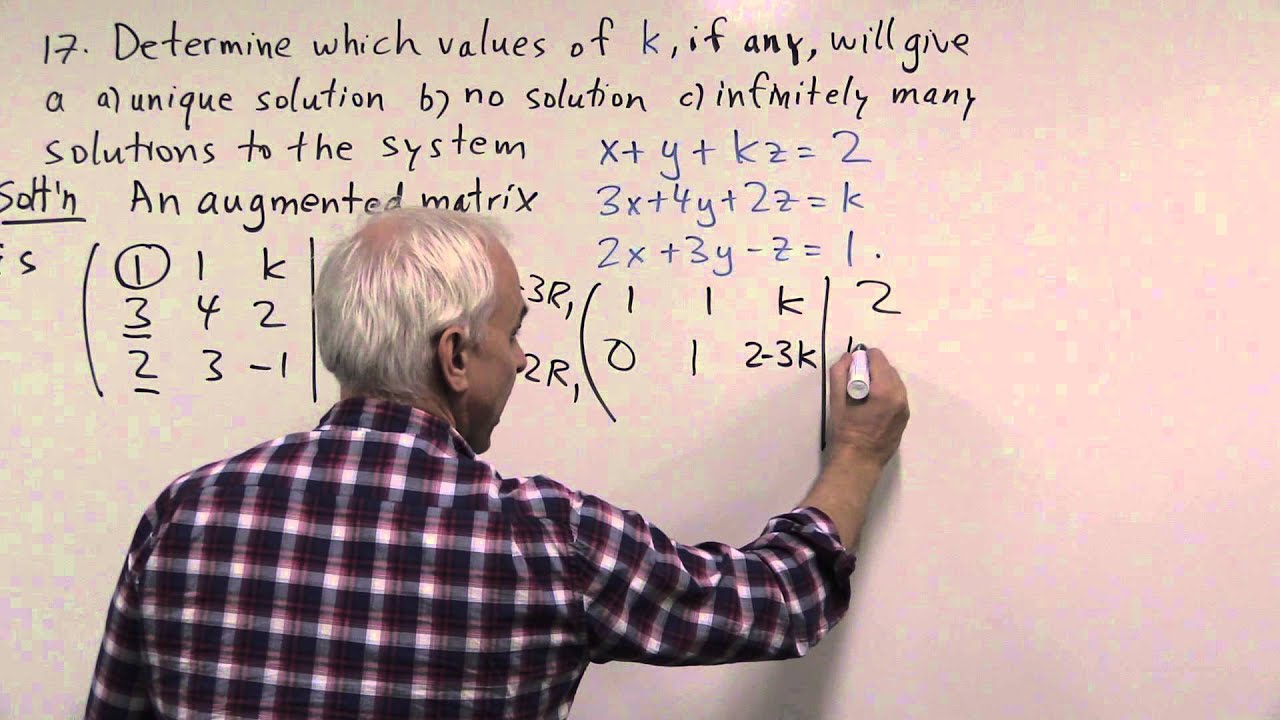
Показать описание
In this problem we determine values of unknown constant k, if any, will give unique solution, no solution infinitely many solutions to the system of equations. Presented by N J Wildberger of the School of Mathematics and Statistics, Faculty of Science, UNSW.
MATH1131 Linear Algebra: Chapter 4 Problem 17
MATH1131 Linear Algebra: Chapter 4 Problem 2 a
MATH1131 Linear Algebra: Chapter 4 Problem 2 b
MATH1131 Linear Algebra: Chapter 4 Problem 2 c
MATH1131 Linear Algebra: Chapter 4 Problem 34
MATH1131 Linear Algebra: Chapter 4 Problem 14 h
MATH1131 Linear Algebra: Chapter 2 Problem 4 i, ii
MATH1131 Linear Algebra: Chapter 1 Problem 41 iv
MATH1131 Linear Algebra: Chapter 3 Problem 66
MATH1131 Linear Algebra: Chapter 5 Problem19
MATH1131 Linear Algebra: Chapter 3 Problem 70
MATH1131 Linear Algebra: Chapter 3 Problem 76
MATH1131 Linear Algebra: Chapter 2 Problem 24
MATH1131 Linear Algebra: Chapter 1 Problem 1
MATH1131 Linear Algebra: Chapter 3 Problem 31
Solving two linear equations (Ch4 Pr3)
MATH1131 Linear Algebra: Chapter 3 Problem 42
solving system of 4 variables (elimination)
MATH1131 Linear Algebra: Chapter 1 Problem 5
Chapter 4-5: Linear Equations with 3 or more variables
MATH1131 Linear Algebra: Chapter 3 Problem 11
MATH1131 Linear algebra: Chapter 2 Problem 1 i
MATH1131 Linear algebra: Chapter 1 Problem 41 i
MATH1131 Overview and Course Information
Комментарии
 0:07:18
0:07:18
 0:08:32
0:08:32
 0:05:33
0:05:33
 0:07:00
0:07:00
 0:05:59
0:05:59
 0:10:15
0:10:15
 0:06:27
0:06:27
 0:07:22
0:07:22
 0:06:29
0:06:29
 0:06:19
0:06:19
 0:10:04
0:10:04
 0:10:30
0:10:30
 0:08:29
0:08:29
 0:10:40
0:10:40
 0:09:19
0:09:19
 0:06:55
0:06:55
 0:05:55
0:05:55
 0:04:24
0:04:24
 0:10:09
0:10:09
 0:09:57
0:09:57
 0:09:00
0:09:00
 0:03:57
0:03:57
 0:04:41
0:04:41
 0:26:56
0:26:56