filmov
tv
Differential Equations: Complex Roots of the Characteristic Equation
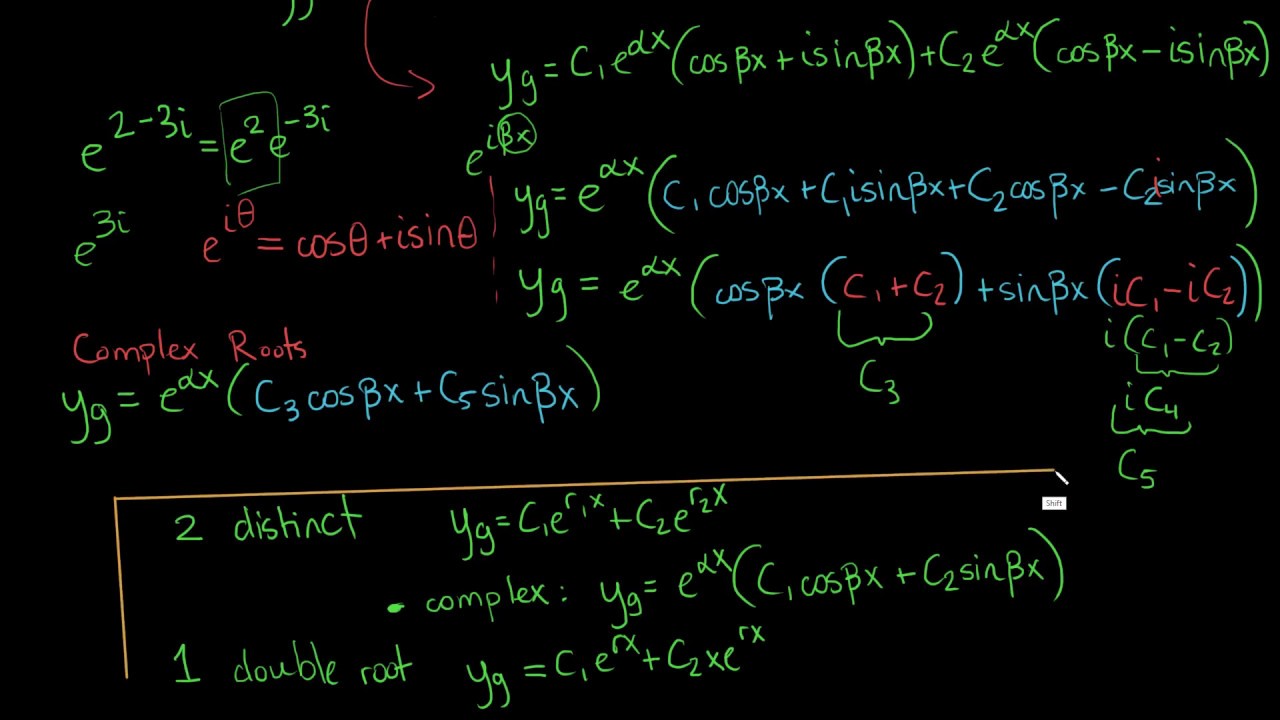
Показать описание
Homogeneous, constant-coefficient differential equations have a characteristic or auxiliary equation. The solution(s) of this equation yield the particular solutions to the homogeneous differential equation which, when combined, produce a general solution. In this video, we explore the case of complex roots. Because the complex roots are necessarily distinct (if they weren't, they'd be real), the formula for distinct roots works. There is, however, a common simplification involving Euler's formula that I discuss in this video.
 0:09:49
0:09:49
 0:04:32
0:04:32
 0:08:48
0:08:48
 0:10:57
0:10:57
 0:12:36
0:12:36
 0:11:50
0:11:50
 0:25:17
0:25:17
 0:09:34
0:09:34
 0:18:50
0:18:50
 0:05:08
0:05:08
 0:03:57
0:03:57
 0:11:09
0:11:09
 0:10:04
0:10:04
 0:19:09
0:19:09
 0:05:52
0:05:52
 0:08:21
0:08:21
 0:11:54
0:11:54
 0:08:31
0:08:31
 0:04:57
0:04:57
 0:08:01
0:08:01
 0:03:40
0:03:40
 0:36:28
0:36:28
 0:03:57
0:03:57
 0:28:18
0:28:18