Basic Modular Arithmetic and Equivalence classes | 13 |

Показать описание

Basic Modular Arithmetic and Equivalence classes | 13 |

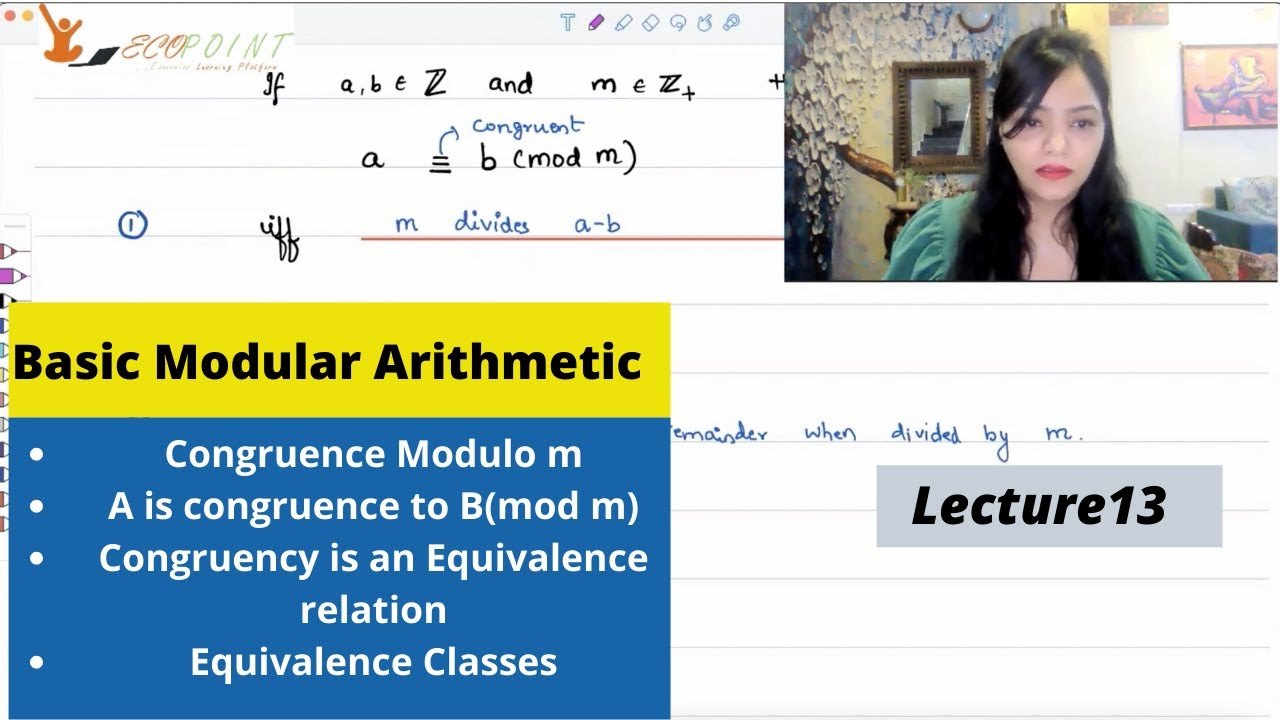
In this lecture we will introduce the concept of Modular Arithmetic and help you understand Equivalence Class.
An equivalence class is the name that we give to the subset of S which includes all elements that are equivalent to each other. “Equivalent” is dependent on a specified relationship, called an equivalence relation. If there’s an equivalence relation between any two elements, they’re called equivalent.

Modular numbers (equivalence classes mod m)
Definition: if a, m ∈ Z then [a]m (called the equivalence class of a mod m) is the set of all integers that are congruent to a, mod m. Often times m will be clear from context, in which case I will omit it and just write [a].

For each nonzero integer n we define a relation on the integers Z called congruence mod n as follows:

two integers a and b are congruent mod n if a−b is divisible by n.

This is equivalent to saying a and b have the same remainder when you divide by n.

For example, 7 and 15 are congruent modulo 4 (as 7-15=-8 is a multiple of 4), but they are not congruent modulo 5 (as 7-15=-8 is not a multiple of 5.)
It is common to write a≡bmodn to mean that a is congruent to b mod n.

congruence modulo n is an equivalence relation.

The set of equivalence classes under congruence modulo n is written Zn.

For example, if n=2 there are exactly two equivalence classes,

[0]={…,−4,−2,0,2,4,…} which is the set of all even numbers

and [1]={…,−3,−1,1,3,…}. which is the set of all odd numbers.
Learning Objectives:
1. Defining Modular Arithmetic
2. Defining Congruence Modulo
3. Defining Equivalence Classes
4. Examples to understand the use

This is useful for all those students who are preparing for any entrance that would test you on the basics of Advance mathematics and calculus, specifically
1. Basics for MA Economics
2. Semester Exam, mathematical methods
3. Indian Economic Services