Distributed loading on a beam example #2: triangular loads

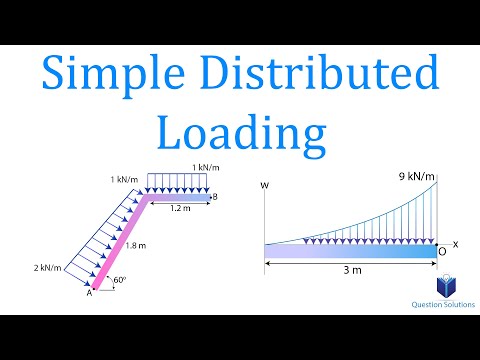
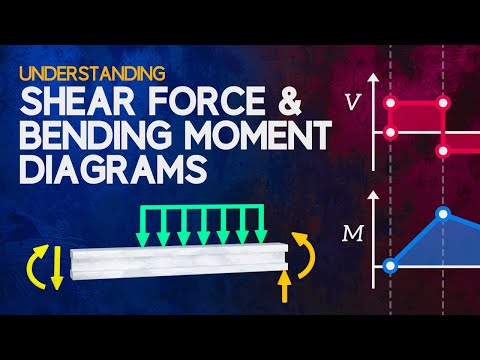
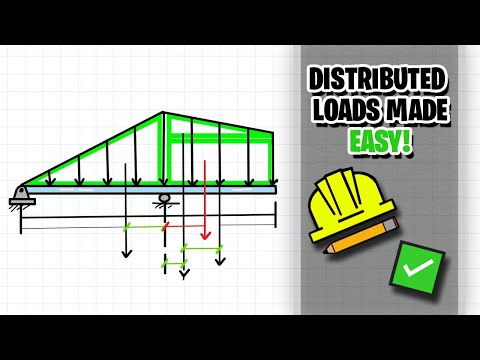
This engineering statics tutorial compares a rectangular (uniformly distributed load) to a triangular distributed load. In both cases, we need to find the resultant force, whose line of action passes through the centroid, and has a magnitude equal to the total distributed load.

If you found this video helpful, please consider supporting my work on Patreon:

Looking for more statics tutorials? Check out all of the videos that I made:

Looking for practice problems with solutions? I also created a whole set of fully solved statics problems with step-by-step hand calculations:

Looking for software? I highly recommend checking out SkyCiv. They make a full suite of online structural analysis software and tools that are useful for both students and professionals, including calculators for beams, trusses, frames, moment of inertia and more. It’s great for checking your work:

Lastly, don’t forget to subscribe on YouTube and join the Engineer4Free mail list:

Thanks for watching, I hope it helps!

[Aguvika]

Can you please explain how KN/m is a measurement of height?? normally we say something is x inches, or x meteres tall.

[briannahoff]

Thank you very much! My statics class is online this semester, and our lectures are basically the teacher telling us to read her notes. It helps so much to see examples worked through!

[francisg]

Amazing and spot-on explanation. I always forget how to find moment with a beam including distributed load, and always relied on symmetry to set reactions equal to each other. This video is much, much appreciated!!

[StenTarvo]

Now i finally understand how it works. Lightbulb went off! Thank you!

[gamzeergun]

before watching your videos I thought I could never pass my statics course in my whole life but you made me feel confident about this course thank youu so muchhhh

[dbs]

thank you so much man, cleared up a lot of confusion. barely got through statics, so mechanics of materials has been pretty tough. always get stuck on figuring out how to plug in a distributed load into the moment equilibrium equation.

[kawaii]

Literally a life savor, having a test on friday and couldnt find anything on triangular load thank you 😭😭😭💞💞

[danielstewart]

This video was everything I needed. Thanks for the upload!

[adamalmuhana]

This video was amazing! Completely helped me solve my problem and other portions of the problem! Thanks!

[anfalal_aboud]

From Iraq, thanks a lot for this effort🤗

[Dasni]

Thank you was struggling with triangular loads until I saw this.

[Hud_Adnan]

I really appreciate your videos, and I wish you the best of all, please continue on your work ... better than most of the university lecturers 🌸🌸🌸

[suhaybmir]

how would you solve it if per say the A and B were not located on each ends. So lets say A is at 2m from the left and b is at 4m from the left.

[eagle]

Why is the centroid of the triangle is at 1/3 ish place of the tall side?

[NuwabiineIvan-muzy]

Thanks Alot, this video helped me really

[WasiqqIsNinja]

honestly a lifesaver, thanks for this!!

[christinagraceduallo]

Why other problems has to multiply to 1/3 and 2/3 I don’t understand. Do you have a link for a video discussing why use 1/3 or 2/3? I don’t know where did they get that some problems even has 1/2 and I don’t know where did they get that

[ubaidshahzad]

How would we know exactly where the point of action? I have a exam on this and based off different triangles, my lecturer will say the point of action is either 1/3 or 2/3 but I am not sure when I would identify the point of action to be either 2/3 or 1/3. Choosing either gives different final answers.

I feel as if my question is not clear but if it is, please clarify. Thank you.

[finnconroy]

Would it not be (1/sqrt2) of the way over, not 2/3rds. Thus would split the load in half

[aliahmed]

is the centroid for a triangular always 2/3rds in