Measure Theory 8 | Monotone Convergence Theorem (Proof and Application) [dark version]

preview_player
Показать описание


Please consider to support me if this video was helpful such that I can continue to produce them :)

🙏 Thanks to all supporters! They are mentioned in the credits of the video :)

This is part 8 of 22 videos.

#MeasureTheory
#Analysis
#Integral
#Calculus
#Measures
#Mathematics
#Probability

I hope that this helps students, pupils and others. Have fun!

(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)

  1. The Bright Side of Mathematics
  2. Mathematics (Field Of Study)
  3. Metric Space
  4. metrischer Raum
  5. Mathematik
  6. Normed Space
Рекомендации по теме
Measure Theory 8 0:12:35

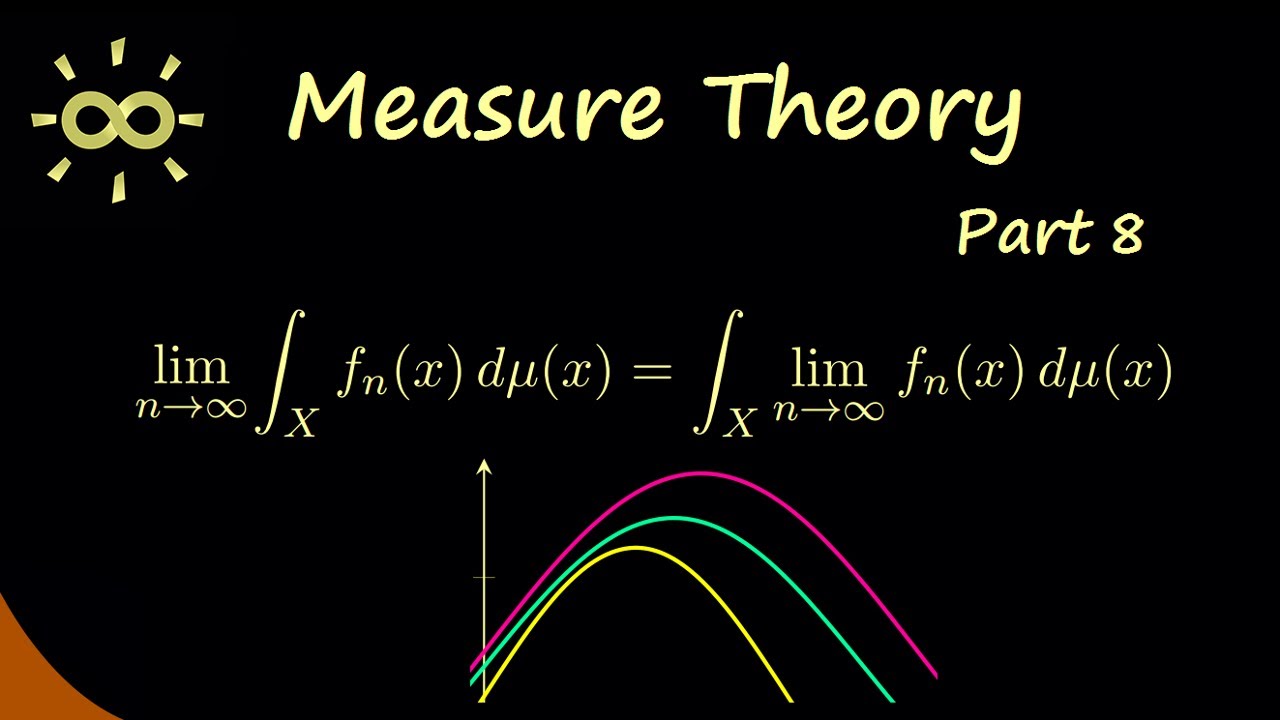
Measure Theory 8 | Monotone Convergence Theorem (Proof and Application)

Measure Theory 8 0:12:50

Measure Theory 8 | Monotone Convergence Theorem (Proof and Application) [dark version]

Measure Theory: Part 0:12:35

Measure Theory: Part 8 Monotone convergence theorem Proof and application

Measure Theory 7 0:19:53

Measure Theory 7 | Monotone Convergence Theorem (and more)

Abstract measure theory: 0:23:13

Abstract measure theory: monotone classes

07-15. Measure theory 0:40:06

07-15. Measure theory and probability - Monotone convergence theorem: complete proof.

UPB Math 232 0:52:22

UPB Math 232 LEC2B Dynkin Systems and Monotone Classes

The Harmonic Series 0:12:34

The Harmonic Series | Illustrated Theory of Music #8

A New Way 0:25:58

A New Way to Measure Sets! (How to build a strictly monotone measure) #SoME2 #3b1b

Probability and Measure, 1:27:41

Probability and Measure, Lecture 7: Lebesgue-Stieltjes Measure and Monotone Classes

Probability and Measure, 1:27:41

Probability and Measure, Lecture 7: Lebesgue-Stieltjes Measure and Monotone Classes

Measure Theory 7 0:20:08

Measure Theory 7 | Monotone Convergence Theorem (and more) [dark version]

Lecture 5. The 0:59:59

Lecture 5. The Lebesgue integral and Monotone convergence theorem.

Monotone convergence theorum 0:08:11

Monotone convergence theorum in measure theory part b Lec #14

Lebesgue Integration 4: 0:17:58

Lebesgue Integration 4: Monotone Convergence Theorem

Measure Theory 3.4: 0:13:11

Measure Theory 3.4: Monotone Convergence Theorem

Fundamental convergence theorems 0:35:50

Fundamental convergence theorems in Lebesgue integration: Monotone convergence theorem, Tonelli&apos...

Monotone Convergence Theorem: 0:11:05

Monotone Convergence Theorem: Explained with graph and examples.

Prove Lebesque's Monotone 0:02:24

Prove Lebesque's Monotone Convergence Theorem, M.SC/PG Semester-2 Paper-VIII(CC-8) measure theo...

FPT Lecture2g - 0:06:17

FPT Lecture2g - Measure theory 101: Theorem of monotone convergence

mod08lec59 - Monotone 0:20:26

mod08lec59 - Monotone Convergence Theorem - 1

Measure Theory: Part 0:19:53

Measure Theory: Part 7 Monotone convergence theorem and more

ST342 051 0:17:08

ST342 051 Monotone and dominated convergence 1 of 3

Prove Lebesgue monotone 0:22:45

Prove Lebesgue monotone convergence theorem, Fatou's lemma, Lebesgue's dominant convergenc...

Комментарии
Автор

Nice lesson!
but I have a doubt.
Isn't it inaccurate to say that the idea is that there is a f_n >= (1-epsilon)h almost everywhere as in the drawing?
if this were the case, uniform convergence would be needed (as in the case of the Reinman integral), right?

In this case it is enough that it is locally, i.e. on the X_n, which is what you use in the proof.
Or am I wrong?

tommasobellanova