How to use the remainder and factor theorem for polynomials

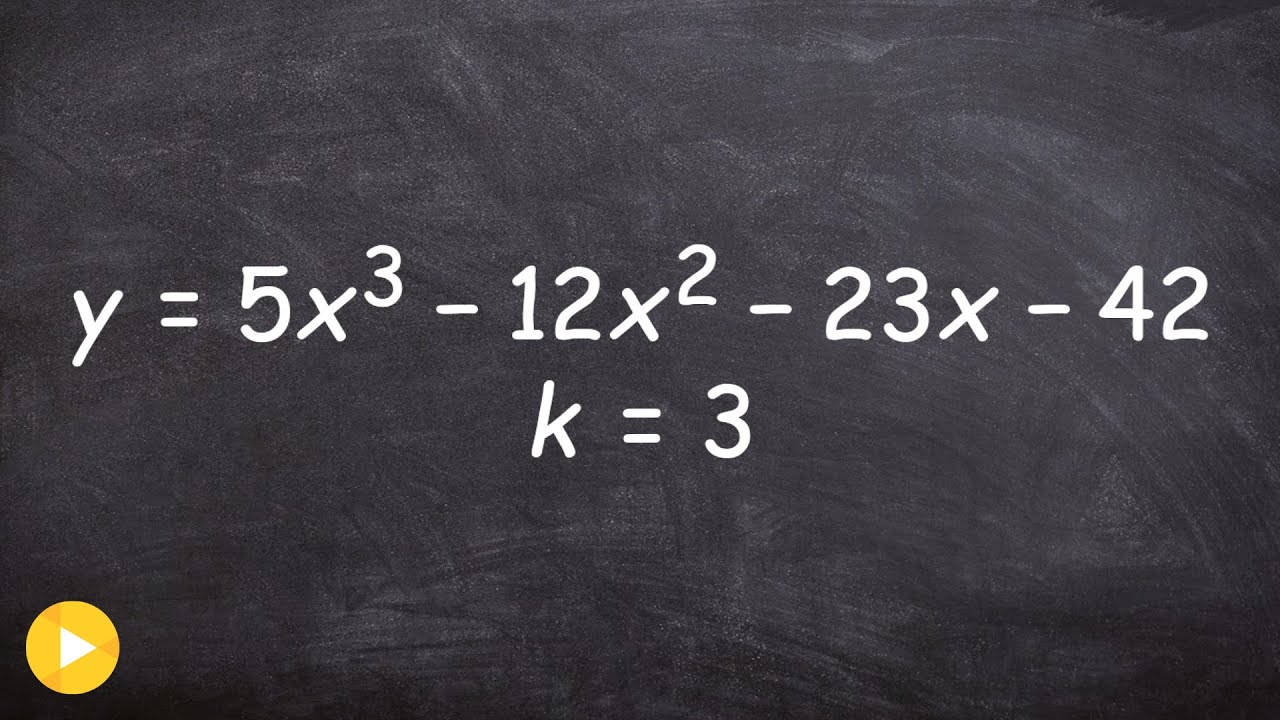
Показать описание

👉 Learn about and how to apply the remainder and factor theorem. The remainder theorem states that f(a) is the remainder when the polynomial f(x) is divided by x - a. Thus, given a polynomial, f(x), which is to be divided by a linear binomial of form x - a, the remainder of the division is given by f(a).

The factor theorem is a special case of the remainder theorem which states that if f(a) = 0, then x - a is a factor of the polynomial f(x). Thus, given a polynomial, f(x), to see if a linear binomial of form x - a is a factor of the polynomial, we solve for f(a). If f(a) = 0, then x - a is a factor, and x - a is not a factor otherwise.

These two theorems help us understand how we better understand the relationship between a polynomial function, its factors, and the remainder. Using the theorem also can save us time from determining if we have a factor or zero of a polynomial without having to use division.

Organized Videos:
✅Remainder and Factor Theorem
✅Remainder and Factor Theorem | Learn About
✅How to apply the Remainder and Factor Theorem

Connect with me:

#polynomials #brianmclogan