filmov
tv
Using the remainder theorem and checking your answer with synthetic division

Показать описание
👉 Learn about and how to apply the remainder and factor theorem. The remainder theorem states that f(a) is the remainder when the polynomial f(x) is divided by x - a. Thus, given a polynomial, f(x), which is to be divided by a linear binomial of form x - a, the remainder of the division is given by f(a).
The factor theorem is a special case of the remainder theorem which states that if f(a) = 0, then x - a is a factor of the polynomial f(x). Thus, given a polynomial, f(x), to see if a linear binomial of form x - a is a factor of the polynomial, we solve for f(a). If f(a) = 0, then x - a is a factor, and x - a is not a factor otherwise.
These two theorems help us understand how we better understand the relationship between a polynomial function, its factors, and the remainder. Using the theorem also can save us time from determining if we have a factor or zero of a polynomial without having to use division.
Organized Videos:
✅Remainder and Factor Theorem
✅Remainder and Factor Theorem | Learn About
✅How to apply the Remainder and Factor Theorem
Connect with me:
#polynomials #brianmclogan
The factor theorem is a special case of the remainder theorem which states that if f(a) = 0, then x - a is a factor of the polynomial f(x). Thus, given a polynomial, f(x), to see if a linear binomial of form x - a is a factor of the polynomial, we solve for f(a). If f(a) = 0, then x - a is a factor, and x - a is not a factor otherwise.
These two theorems help us understand how we better understand the relationship between a polynomial function, its factors, and the remainder. Using the theorem also can save us time from determining if we have a factor or zero of a polynomial without having to use division.
Organized Videos:
✅Remainder and Factor Theorem
✅Remainder and Factor Theorem | Learn About
✅How to apply the Remainder and Factor Theorem
Connect with me:
#polynomials #brianmclogan
Remainder Theorem and Synthetic Division of Polynomials
What is the Remainder Theorem
Polynomial remainder theorem | Polynomial and rational functions | Algebra II | Khan Academy
Remainder & Factor Theorem (1 of 2: How do we calculate remainders without dividing?)
Remainder Theorem by Long Division
How to Use the Remainder Theorem
Quick and Easy Way to Find the Remainder of a Polynomial - Use the Remainder Theorem!
How does the remainder theorem work with polynomials
Solving A-Level Math 9709 Past Paper | Factor & Remainder Theorem Explained
How to use the Remainder Theorem with Polynomials
Remainder Theorem
Taylor's Remainder Theorem
Remainder Theorem & Factor Theorem | CBSE Class 9 Maths Chapter 2 | NCERT Class 9th Maths
Learn How to Use the Remainder Theorem and Synthetic Division to Find a Function Value
Using the remainder theorem and checking your answer with synthetic division
The Remainder Theorem - How to Find the Remainder when Dividing Polynomials?
Factor Theorem and Synthetic Division of Polynomial Functions
Synthetic Division and Remainder Theorem
Use the Remainder Theorem to Find the Function Value which is the Remainder after Synthetic Division
The Remainder Theorem - Example 1
Polynomial Example: Problem involving Factor Theorem and Remainder Theorem
10 - The Remainder Theorem of Synthetic Division & Polynomial Long Division - Part 1
Remainder Theorem
Using the remainder theorem to evaluate a polynomial function
Комментарии
 0:10:34
0:10:34
 0:04:36
0:04:36
 0:06:42
0:06:42
 0:08:39
0:08:39
 0:02:37
0:02:37
 0:02:41
0:02:41
 0:03:58
0:03:58
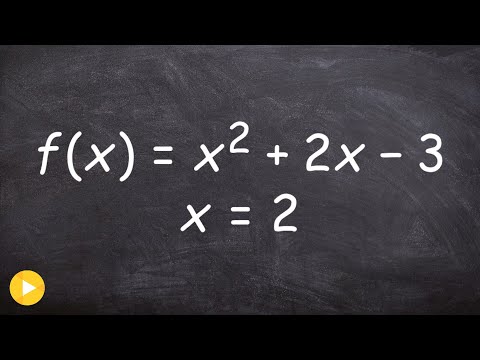 0:03:54
0:03:54
 0:06:23
0:06:23
 0:05:57
0:05:57
 0:08:56
0:08:56
 0:14:08
0:14:08
 0:01:19
0:01:19
 0:02:23
0:02:23
 0:04:53
0:04:53
 0:13:46
0:13:46
 0:10:56
0:10:56
 0:10:49
0:10:49
 0:01:48
0:01:48
 0:04:45
0:04:45
 0:08:13
0:08:13
 0:23:18
0:23:18
 0:52:16
0:52:16
 0:02:47
0:02:47