filmov
tv
By using MI prove that 1²+2²+3²+....+n²=(n(n+1)(2n+1))/6
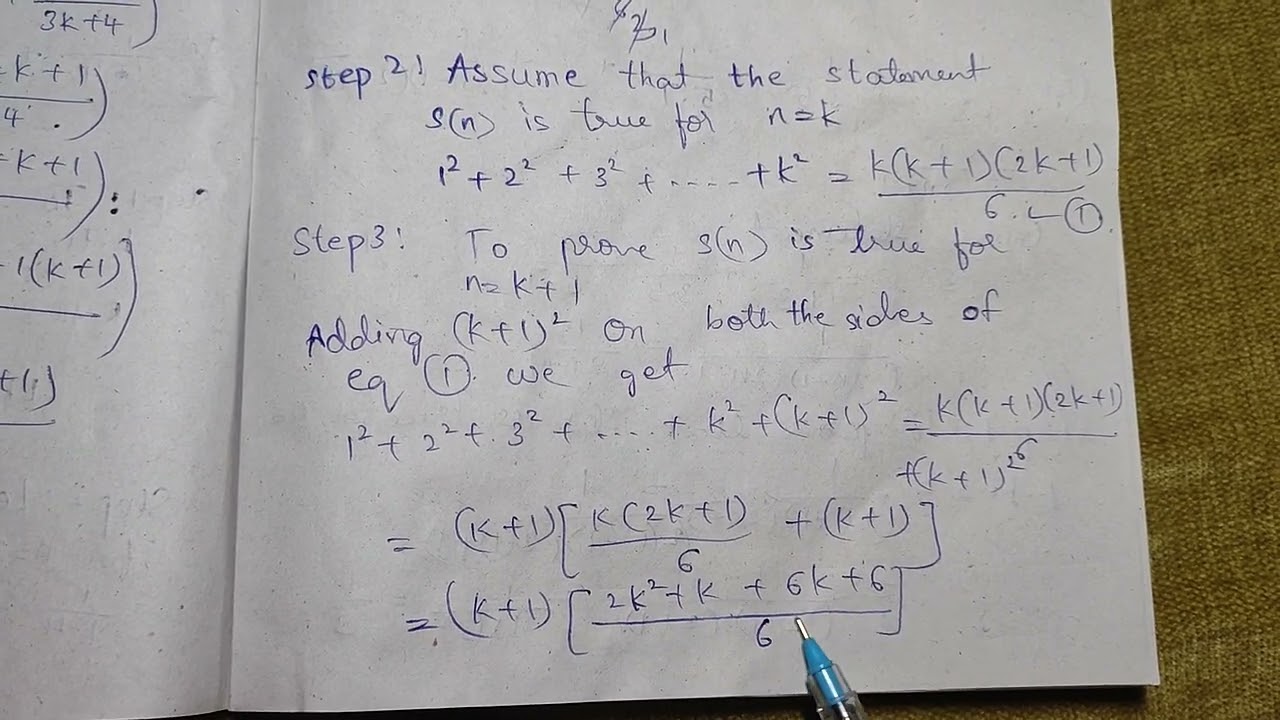
Показать описание
By using MI prove that 1²+2²+3²+....+n²=(n(n+1)(2n+1))/6
How to prove infinitely many things - Mathematical Induction
Prove that 2^n is greater than n for all positive integers n | Mathematical Induction | Maths
Learn how to use mathematical induction to prove a formula
Use MI to prove 1/(1×4 )+1/(4×7)+1/(7×10)+........=n/(3n+1) for all n€ N
Use MI to prove 1³+2³+....n³= n²(n+1)²/4 Part1
Use MI to prove 1/1×3+ 1/3×5+1/5×7+.......+ 1/((2n-1)(2n+1))= n/(2n+1)
Prove by Mathematical Induction. Sum = n/n+1
Prove that 1+2+3+.....n=(n(n+1))/(2) | 10 | MATHEMATICAL INDUCTION AND BIONOMIAL THEOREM | MATH...
Using induction to prove that the sum formula works for any term
Learn to use induction to prove that the sum formula works for every term
Prove the following by the principle of induction | 1^2 + 3^2 + 5^2 +…..+ (2n-1)^2 = n(2n-1)(2n+1)/3...
Prove by the principle of Mathematical induction |1/1.2 + 1/2.3 + 1/3.4 + …… + 1/(n(n+1)) = n/(n+1)...
Use MI to prove 2+3.2+4.2²+.... till n terms =n2^n for all n€N
Use MI to prove 1²+3²+5²+....+(2n-1)²=n(2n-1)(2n+1)/3 Part-2
Prove by induction, Sum of the first n cubes, 1^3+2^3+3^3+...+n^3
Prove by the principle of Mathematical induction | 1^3 + 2^3 + 3^3 + …. + n^3 == [(n(n+1))/2]^2
Prove by Induction that 2 + 4 + 6 + ... + 2n = n(2n − 1)
Learn to use induction to prove the sum formula of a series
Prove by the principle of induction | (1+1/3)(1+ 5/4)(1+7/9) …. (1+ 2n+1/n^2) = (n+1)^2
1. Principle of Mathematical Induction || Prove by Mathematical Induction #mathematicalinduction
Prove that (1 + 3/1) (1 + 5/4) (1 + 7/9) ..... (1 + 2n+1/n^2) = (n + 1)^2
Prove by the principle of Mathematical induction |1/2.5 + 1/5.8 + 1/8.11 +… + 1/(3n-1)(3n+2)=n/6n+4...
Using mathematical induction to prove a formula
Комментарии
 0:05:02
0:05:02
 0:17:35
0:17:35
 0:07:30
0:07:30
 0:07:08
0:07:08
 0:07:28
0:07:28
 0:07:48
0:07:48
 0:05:21
0:05:21
 0:08:22
0:08:22
 0:04:45
0:04:45
 0:04:42
0:04:42
 0:06:29
0:06:29
 0:11:03
0:11:03
 0:08:28
0:08:28
 0:05:02
0:05:02
 0:06:37
0:06:37
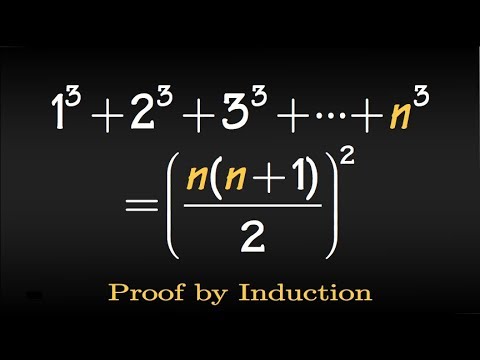 0:09:03
0:09:03
 0:09:07
0:09:07
 0:02:19
0:02:19
 0:06:32
0:06:32
 0:10:41
0:10:41
 0:11:47
0:11:47
 0:09:24
0:09:24
 0:10:28
0:10:28
 0:05:29
0:05:29