filmov
tv
Quotient Rule Made Easy! (applying the quotient rule formula) | Jake's Math Lessons

Показать описание
Quotient Rule Made Easy! (applying the quotient rule formula) | Jake's Math Lessons
Quotient Rule Made Easy! (applying the quotient rule formula) | Jake's Math Lessons
In today's video I'm going to be showing you quotient rule made easy. I'm going to break down the quotient rule in as simple of terms as possible and show you how to use the quotient rule formula. And also how you can remember the quotient rule formula so you can do this on your own on a test or something.
Well, if you want to boost your calculus scores and keep doing well throughout the rest of the turn be sure to hit that subscribe button down below and that bell icon so you're notified of my new videos. So without further ado let's go ahead and jump into the example. I hope by the end of this video you'll be feeling a lot better about the quotient rule.
The problem which I am going to discuss,
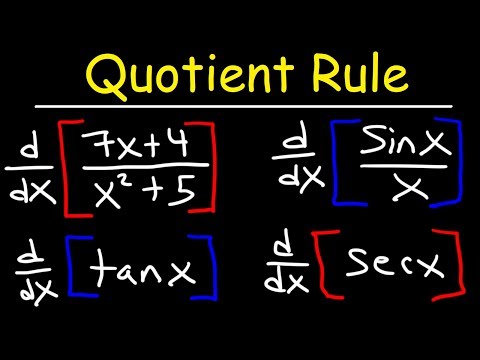
Differentiate h(t) = 2t / (4+t^2)
Watch the whole video carefully to understand the formula easily.
Chapters,
0:00 Introduction
0:38 The problem
0:58 The shortcut formula
1:34 Figuring out hi & lo
1:56 Finding derivatives of hi and lo
2:50 plugging the values in the formula
3:22 Simplification
5:05 Solve for the problem
••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••
YOU MIGHT ALSO BE INTERESTED IN...
••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••
Some links in this video description may be affiliate links meaning I would get a small commission for your purchase at no additional cost to you.
Your queries,
quotient rule,quotient rule made easy,derivatives,product rule,chain rule,how to use quotient rule,quotient,rule,derivative,quotient rule calculus,derivatives quotient rule,quotient rule derivatives,derivative rules,derivative quotient rule,quotient rule differentiation,quotient rule harder derivatives example,calculus practice problems,calculus homework help,how to use the quotient rule calculus,calculus differentiation rules,derivative formulas,calculus
Quotient Rule Made Easy! (applying the quotient rule formula) | Jake's Math Lessons
In today's video I'm going to be showing you quotient rule made easy. I'm going to break down the quotient rule in as simple of terms as possible and show you how to use the quotient rule formula. And also how you can remember the quotient rule formula so you can do this on your own on a test or something.
Well, if you want to boost your calculus scores and keep doing well throughout the rest of the turn be sure to hit that subscribe button down below and that bell icon so you're notified of my new videos. So without further ado let's go ahead and jump into the example. I hope by the end of this video you'll be feeling a lot better about the quotient rule.
The problem which I am going to discuss,
Differentiate h(t) = 2t / (4+t^2)
Watch the whole video carefully to understand the formula easily.
Chapters,
0:00 Introduction
0:38 The problem
0:58 The shortcut formula
1:34 Figuring out hi & lo
1:56 Finding derivatives of hi and lo
2:50 plugging the values in the formula
3:22 Simplification
5:05 Solve for the problem
••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••
YOU MIGHT ALSO BE INTERESTED IN...
••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••
Some links in this video description may be affiliate links meaning I would get a small commission for your purchase at no additional cost to you.
Your queries,
quotient rule,quotient rule made easy,derivatives,product rule,chain rule,how to use quotient rule,quotient,rule,derivative,quotient rule calculus,derivatives quotient rule,quotient rule derivatives,derivative rules,derivative quotient rule,quotient rule differentiation,quotient rule harder derivatives example,calculus practice problems,calculus homework help,how to use the quotient rule calculus,calculus differentiation rules,derivative formulas,calculus
Комментарии
 0:05:26
0:05:26
 0:08:51
0:08:51
 0:25:26
0:25:26
 0:11:55
0:11:55
 0:07:02
0:07:02
 0:22:48
0:22:48
 0:02:55
0:02:55
 0:07:28
0:07:28
 3:01:36
3:01:36
 0:07:53
0:07:53
 0:00:57
0:00:57
 0:01:00
0:01:00
 0:01:00
0:01:00
 0:27:15
0:27:15
 0:00:53
0:00:53
 0:11:53
0:11:53
 0:11:18
0:11:18
 0:23:36
0:23:36
 0:04:23
0:04:23
 0:11:44
0:11:44
 0:00:59
0:00:59
 0:10:35
0:10:35
 0:00:57
0:00:57
 0:03:20
0:03:20