filmov
tv
Solve (a to 4th – 3a squared – 4 = 0) How Much Algebra Do You Know? Polynomial Equations
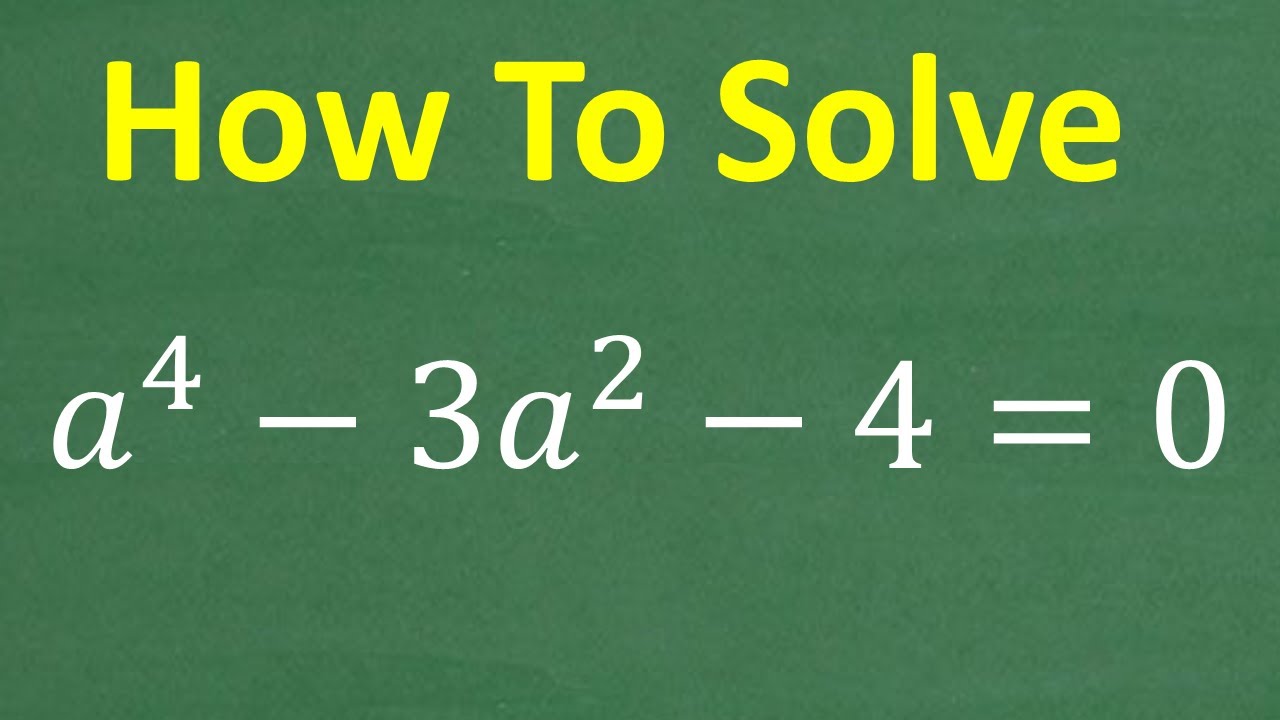
Показать описание
Help with Middle and High School Math
Test Prep for High School Math, College Math, Teacher Certification Math and More!
Popular Math Courses:
Math Foundations
Math Skills Rebuilder Course:
Pre-Algebra
Algebra
Geometry
Algebra 2
Pre-Calculus
• MIDDLE & HIGH SCHOOL MATH
• HOMESCHOOL MATH
• COLLEGE MATH
• TEST PREP MATH
• TEACHER CERTIFICATION TEST MATH
How to Solve a Rubik’s Cube in 4 Moves (Impress Your Friends)
Easiest Solve for Rubik's Cube | Step 4 | Beginners Guide
4 by 4 rubik's cube trick solve(easiest)...#shorts
Can you solve a 4 move scramble? | NEXcube
HOW TO SOLVE RUBIK'S CUBE IN 4 MOVES!
Can You Solve The 4 Hats Logic Puzzle?
Solving a 2x2 Mini Rubik's Cube 4 Square
Can you solve this 4th grade problem?
Solve 5(2-x)+3(x+6)=10-4(6-2x): Linear Equation Video Solution | Tiger Algebra
Tower of Hanoi 4 Disc Solution in the Fewest Moves
4 Steps in Solving Problems
How to Solve a 4th Degree Polynomial in Calculator (991-ES & 991-MS)
Solving A Very Special Quartic | x^4+1=0
Plus One Maths Christmas Exam | 50 Sure Questions | Exam Winner Plus one
4 bands Puzzle Ring solution - Leonardo Leather and Gold
How to solve a Rubik’s Cube Step 4 The Middle Layer
How to solve a Rubik’s cube | The Easiest tutorial | Part 4
Solve 4 Equations And 4 unknowns | Easiest way to solve [ English ]
HOW TO SOLVE QUARTIC EQUATION || HOW TO SOLVE FOURTH DEGREE EQUATION || QUARTIC EQUATION PROBLEM
Puzzle Ring Solution for 4ASL 4 Band Sterling Silver Puzzle Ring
Can you Solve Fourth Degree Quadratic Equations in Less than 1 Minute?
4 BANDS PUZZLE RING SOLUTION
Key 47! 4 September How to Solve Mini Game PUZZLE in Hamster Kombat (100% SOLVED!)
How to Solve a Fourth Degree Polynomial Equation x^4 - 2x^3 - 5x^2 + 8x + 4 = 0
Комментарии
 0:00:58
0:00:58
 0:38:11
0:38:11
 0:00:25
0:00:25
 0:00:34
0:00:34
 0:01:26
0:01:26
 0:04:39
0:04:39
 0:09:32
0:09:32
 0:09:24
0:09:24
 0:02:53
0:02:53
 0:01:01
0:01:01
 0:03:50
0:03:50
 0:01:01
0:01:01
 0:00:46
0:00:46
 3:36:07
3:36:07
 0:02:39
0:02:39
 0:00:55
0:00:55
 0:10:03
0:10:03
 0:09:21
0:09:21
 0:04:42
0:04:42
 0:04:23
0:04:23
 0:08:38
0:08:38
 0:01:04
0:01:04
 0:00:50
0:00:50
 0:10:59
0:10:59